Triominoes
Problem
A triomino is a flat L shape made from 3 square tiles.

A chess board is marked into squares the same size as the tiles and just one square, anywhere on the board, is coloured red.
Chess boards for this game are of size 2 k by 2 k where k is any whole number
For example 2 by 2, 4 by 4, 8 by 8 etc.
The aim is to cover the board with triominoes, not overlapping, so that only the red square, wherever it is, is exposed. Is this possible? Investigate. Explain.
Student Solutions
In order to show that all chessboards of size 2 k by 2 k will have a total number of squares that is 1 more than a multiple of 3, we have to show that the total numbers of squares equals 1(modulo 3). To show this we use the fact that 2 k can only be equal to 1 or 2 (modulo 3), as 2 k is not a multiple of 3 (so 2 k cannot equal 0).
If
If
Therefore, I have proved that all chessboards of size 2k by 2k will have a total number of squares, which is 1 more than a multiple of 3.
Another way of thinking about it is this:
The smallest chessboard, 2 1 by 2 1, has 4 squares, which will be covered by one triomino and an empty red square.
The next chessboard, 2 2 by 2 2, is four times bigger, since both the length and the width have been doubled; this means that I will have four times as many triominoes and four empty red squares - but three of these red squares can be covered by another triomino, which leaves only one empty red square.
The next chessboard will again be four times bigger, so the process repeats itself again and again and again.
If we start with a chessboard that is 1 more than a multiple of 3 (eg. 3x + 1) and multiply it by 4, we will end up with another number which is 1 more than a multiple of 3:
4 (3x + 1) = 12x + 4 = 3 (4x + 1) +1

After some experiments, I found out a certain answer.
We start with a 4 by 4 square. I find that the red square can be any of the 16 squares, as the 4 by 4 square can be divided into four 2 by 2 squares as shown:
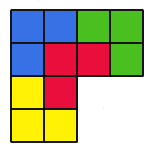
Therefore, the last remaining square can be made up of the red square, which could be any one of the 4 squares there, and a triomino. Therefore, a 4 by 4 square is possible.
However, the large square can be rotated around, so the square removed can be anyone of the 4. Therefore, the red square could be any of the 16 squares in a 4 by 4 square.
Let's look at the 8 by 8 square next. I divide the 8 by 8 square into four 4 by 4 squares. Suppose the red square is in square A:
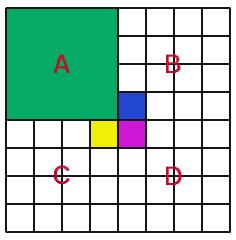
This has already been shown earlier in the 4 by 4 square problem. Next, we need to show that the other three squares (B, C and D) can be filled by triominoes, leaving the 3 coloured squares empty. This is very easy, as we take each of the three squares individually and use the method mentioned above for a 4 by 4 square. We can now fill the three coloured squares with another triomino. Therefore, all the squares in B, C and D are covered with triominoes, and all the squares in A are possible empty red squares.
Remember that A rotated and flipped can become B, C and D. Therefore, an 8 by 8 square can have all its 64 squares as empty red squares.
Let's look at the 16 by 16 square next. I divide the 16 by 16 square into four 8 by 8 squares. Suppose the red square is in square A:
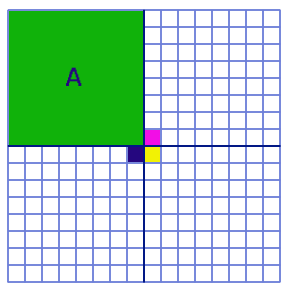
This has already been shown earlier in the 8 by 8 square problem. Next, we show that the other three 8 by 8 squares can be filled by triominoes, leaving out the 3 coloured squares. This is very easy, as we take the 3 squares individually, and using the method mentioned above, show that the coloured squares can be left out in each of the three 8 by 8 squares. Therefore, all the squares in A are possible empty red squares.
Remember that A can be rotated and be placed in any quarter of the 16 by 16 square. Therefore, a 16 by 16 square can have all its 256 squares as empty red squares.
This pattern continues until infinity, since each chessboard will be 4 times bigger than the previous, so the proof for the previous chessboard can always be used for the next one.
[Notice that this is a geometric representation of
4 (3x + 1) = 12x + 4 = 3 (4x + 1) +1
that was mentioned at the beginning]
School: Raffles Institution
Country: Singapore
