T for tan
Can you find a way to prove the trig identities using a diagram?
Problem
Consider a right angled triangle with an acute angle of $\theta$. Let the base of the triangle be of length 2.
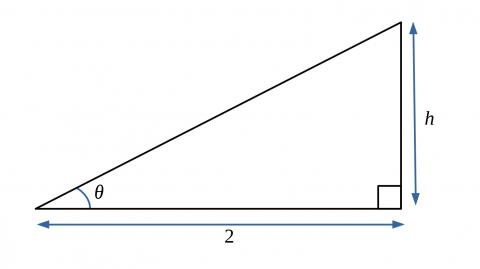
Find the height of the triangle in terms of $t$, where $t=\tan \theta$.
Now imagine a line in the triangle which forms an isosceles triangle with two angles equal to $\theta$.
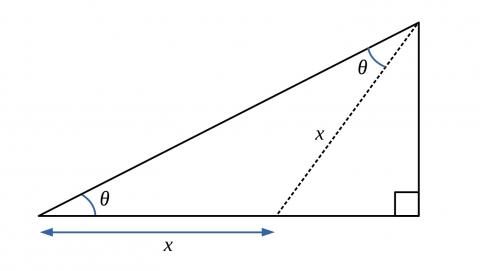
Use this diagram to prove the double angle formula, where $t=\tan \theta$: $$\tan2\theta = {2t\over {1-t^2}}, \quad \sin2\theta = {2t\over {1+t^2}},\quad \cos2\theta = {{1-t^2}\over {1+t^2}}$$
Getting Started
The height of the triangle is equal to $2 \tan \theta = 2t$.
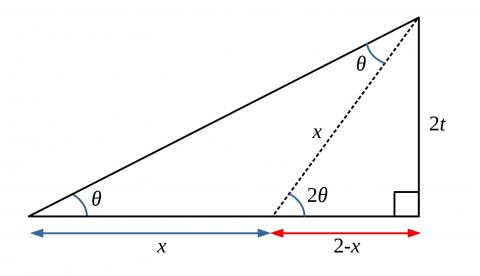
Can you use the smaller right angled triangle to find $x$ in terms of $t$?
Student Solutions
Well done to Dylan from Brooke Weston, Joshua from Bohunt Sxth Form, Mykhailo and Daniel, Ilan, Adam and Alexander from JFS, Soumya from King's Maths School, Josh from Queen Elizabeths Grammar School Alford, Bertie from Sir William Borlase's Grammar School, Isy and Rafi, all in the UK, and to DongYeon, who all used Pythagoras' Theorem first to solve the problem. Here is Dylan's work:
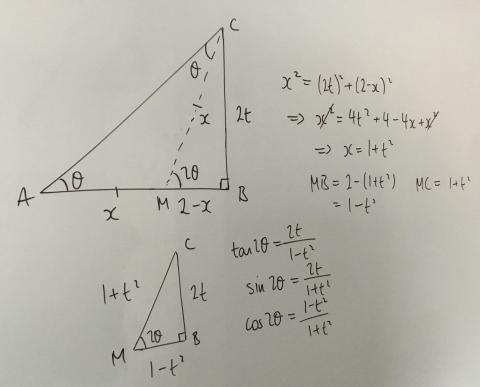
Three mathematicians from Simon Balle All-through School wrote a two-page paper explaining their work. They used a slightly different method. You can download their paper here.
DongYeon suggested generalising the problem:
This will work for any right triangle of any length. Let's use a variable $L$ instead of $2.$
$h = L\tan \theta$
$(Lt)^2 + (L - x)^2 = x^2$
$x = \dfrac{L(1 + t^2)}2$
$L - x = \dfrac{L(1 - t^2)}2$
$\tan{2\theta} = \dfrac h{(L - x)} = \dfrac{Lt}{\frac{L(1 - t^2)}{2}} = \dfrac{2t}{1 - t^2}$
$\sin{2\theta} = \frac hx = \dfrac{Lt}{\frac{L(1 + t^2)}{2}} = \dfrac{2t}{1 + t^2}$
$\cos{2\theta} = \dfrac{L - x}x = \dfrac{\frac{L(1 - t^2)}2}{\frac{L(1 + t^2)}{2}} = \dfrac{1 - t^2}{1 + t^2}$
Note that this is not necessary: using $2$ rather than $L$ did not mean that $\tan{2\theta}=\dfrac{2t}{1 - t^2}$ is only true for triangles where one side is less than $2$. It is true for all acute values of the angle $\theta .$ So in this case, you can prove the formula using a side of length $L,$ or of any other length. When this is the case, it is often most efficient to choose a simple number, like $1$ or $2.$
Teachers' Resources
This problem asks students to use a right-angled triangle to derive expressions for $\tan 2 \theta$, $\sin 2 \theta$ and $\cos 2 \theta$ in terms of $\tan \theta$.
Students will need to use:
- Angle sum of triangle
- Pythagoras's theorem
- Right-angled trig
You can download a Word and PDF version of this problem.
Students who are studying matrices might like to see how this result is used in the problem Reflect Again.
