Sweetie box
Problem
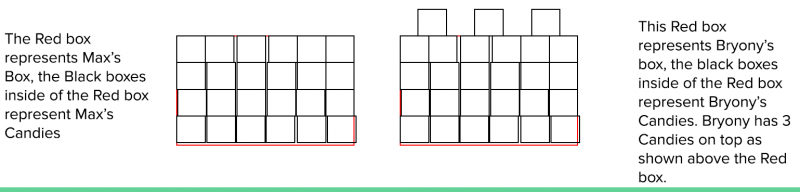
Below, you can see two boxes.
|
Max's box |
Bryony's box |
The box on the left is Max's. All of Max's sweets are in that box.
The box on the right hand is Bryony's. Bryony's sweets are in that box and there are also three more sweets on top of her box.
Each box has exactly the same number of sweets inside.
What do you know about the number of sweets each child has?
We would love to hear your ideas. You may like to use drawings, writing, numbers, symbols... to help show your thinking.
This task has been inspired by a book chapter written by Carraher, Schliemann and Schwartz (2007).
Student Solutions
We were sent lots of different ideas about this challenge, so thank you to everybody who sent a solution in.
Saif from Pierrepont Gamston Primary School in England said:
We know that Bryony has more sweets than Max because if they have the same amount of sweets in each box Bryony would still have the 3 extra sweets on top of her box so she will have more.
Well done Saif - can we say anything about how many more sweets Bryony will have compared to Max?
Owen from Stoke Bishop Primary School in England thought about how many sweets Max and Bryony could have in total:
If it's an even number in the box it is doubled, add 3 gets an odd number. But an odd number doubled is an even number, if you add 3 you also get an odd number. So Max and Bryony have an odd number of sweets total but we don't know if they each have an odd or an even number.
Thank you for those ideas, Owen - it's always interesting to think about whether numbers might be odd or even.
Hugh from Dame Bradbury's in England thought about the numbers of sweets in terms of percentages:
If Max had ten sweets and 100%. Bryony would have 13 sweets and 130%.
Well done Hugh! Think about what would happen if Max had a hundred sweets in his box instead - will the percentages still be 100% and 130%?
Nate from Pierrepont Gamston Primary School represented the number of sweets in a box with algebra:
Bryony will always have three more sweets than Max. If we say the number of sweets inside their boxes is X, then Max will have X and Bryony will have X+3.
Thank you for that idea, Nate. When we don't know one of the numbers in a question, it's sometimes helpful to use a picture or a letter to represent that number.
Some children used estimation to work out how many sweets might be in each box. Sara and Kate from University of Chicago Laboratory Schools in the USA sent in this explanation:
Bryony has 3 more candies than Max because they have the same amount of candies in their boxes and Bryony has 3 extra candies on top.
The box seems to hold about 24 candies because the box is 1 inch tall and 1.5 inches wide (when it appears on-screen), the candies are 1/4 inch by 1/4 inch. Therefore 6 candies can fit across and there can be 4 stacks of 6, and 4 times 6 is 24. This is all assuming that the box only consists of the (type of) candies on top and that they are all the same size.
Max has 24 candies because of the thinking shown above and Bryony has 27 candies because 24 plus 3 is 27.
Thank you for that clear explanation, Sara and Kate. Have a look at the pictures they've used to represent the boxes of sweets. Can you see why they think there might be 24 sweets in each box?
Lots of other children from the University of Chicago Laboratory Schools also sent in their ideas about how to estimate the number of sweets in each box. Emma, Saidie and Ellie noticed that the box is actually 3D, and they pointed out that there might be more layers of sweets behind the front layer. How could this change the number of sweets in Sara and Kate's estimation in the picture above?
If you have any other ideas about how many sweets Max and Bryony might have, we'd love to hear from you. Please email us with your ideas.
Teachers' Resources
Sweetie Box
Below, you can see two boxes.
|
Max's box |
Bryony's box |
The box on the left is Max's. All of Max's sweets are in that box.
The box on the right hand is Bryony's. Bryony's sweets are in that box and there are also three more sweets on top of her box.
Each box has exactly the same number of sweets inside.
What do you know about the number of sweets each child has?
We would love to hear your ideas. You may like to use drawings, writing, numbers, symbols... to help show your thinking.
This task has been inspired by a book chapter written by Carraher, Schliemann and Schwartz (2007).
Why do this problem?
This task offers multiple possibilities (and therefore also links to our A Flexible Approach to Calculating feature). It provides an opportunity to consider particular examples and make generalisations. It is also a great way to draw learners' attention to the idea of what can change and what stays the same in a problem context. In addition, the task gives the chance to discuss the tension between realistic considerations and theoretical possibilities. (You may need two lessons to get the most out of it.)
This problem and the possible approach below have been inspired by a book chapter written by Carraher, Schliemann and Schwartz called 'Early algebra is not algebra early'. The full reference and a PDF of the chapter are included at the foot of this page.
Possible approach
Ideally, introduce the problem with two real boxes and real sweets. (Of course you could replace sweets with an alternative item, for example marbles, small toy figures, conkers, counters... but ideally choose something which the children in your class might covet!) State clearly that each box has exactly the same number of sweets inside it, but one box has an extra three sweets on top. Pose the question, "What do you know about the number of sweets each child has?".
Allow a few minutes for learners to think on their own before suggesting they share their ideas with a partner. Facilitate a general class discussion so they have an opportunity to share their initial thoughts. You may find that learners would like to handle the boxes, so pass them round if that is the case. Some children will be wonderfully imaginative and many are likely to offer a specific example. Try to welcome all contributions and ideas.
Next, invite all pairs to record on paper what they know about the number of sweets that Bryony and Max have. Encourage any kind of recording, whether writing, drawing, numbers, symbols..., or a combination of several of these. As the children work, wander round the room to listen and observe. You may notice some pairs:
- record a specific number
- depict a specific number but suggest other possibilities if you engage them in conversation
- keep options open
- begin to express known relationships, for example 'if we take 3 sweets away from Bryony, they would have the same', or 'Bryony has 3 more sweets than Max'
- use a question mark to stand for the unknown quantity and include a guess.
Bring everyone together and draw up a table on the board, similar to this:
| Name | Number of sweets Bryony has | Number of sweets Max has |
Encourage learners to suggest possible values and enter them in the table alongside their name. Although it might seem odd to focus on particular cases at this stage, it provides an opportunity to highlight the fact there are many possible solutions. It also encourages learners to notice and comment on the relationships which are always true (for example, that Bryony always has three more sweets than Max), which in turn provides a checking mechanism for suggested solutions. As individuals or pairs offer an example to add to the table, encourage everyone to consider it carefully and to comment and articulate their reasoning where appropriate.
When incorrect solutions are suggested, encourage learners to explain why they are not possible. Try to ensist on water-tight reasoning. By talking through the fact that, for example, if Bryony has eight sweets, Max cannot have seven sweets, generalities emerge. Although Bryony and Max could in principle have any amount, once an amount is assigned to one of them, the other amount can no longer be anything.
Some children may bring likelihood into the discussion, suggesting that we would be extremely surprised if Bryony had 100 sweets. This is a fantastic opportunity to highlight the tension between mathematical possibilities and realistic considerations.
Key questions
What do you know?
How many sweets might Bryony/Max have?
What can you say for certain?
Possible support
Learners might benefit from having some concrete objects to manipulate as they try out ideas. It may be appropriate to scribe for some children as they talk through their representation.
Possible extension
The task Lots of Lollies could be offered as a follow-up.
Reference:
Carraher, D.W., Schliemann, A.D. and Schwartz, J. (2007). Early algebra is not the same as algebra early. In J. Kaput, D. Carraher and M. Blanton (Eds.), Algebra in the Early Grades. Mahwah, MJ, Erlbaum, pp. 235-272.
You can read the chapter in full here: https://www.researchgate.net/publication/304824539_Early_algebra_algebra_early