Strike a chord
Can you work out the radius of a circle from some information about a chord?
Age
14 to 16
Challenge level
Problem
Image
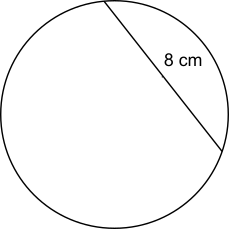
On a circle, there is a chord which has length 8 cm.
The shortest distance from the chord to the centre of the circle is 3 cm.
Find the radius of the circle.
This problem is taken from the World Mathematics Championships
Student Solutions
This diagram shows the information in the question.
Image
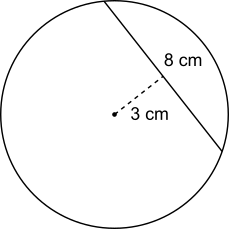
The angle between the 3 cm line segment and the chord must be a right angle, because the 3 cm line segment joins the centre to the closest point on the chord. This means that drawing on a radius can create a right-angled triangle, as shown below:
Image
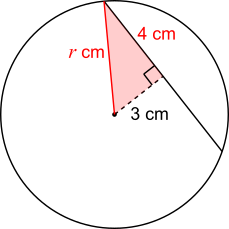
So, by Pythagoras' Theorem, $$\begin{align}3^2+4^2&=r^2 \\
\Rightarrow 9+16&=r^2\\
\Rightarrow 25&=r^2\\
\Rightarrow 5&=r\end{align}$$