Stairs
Problem
Let's suppose that you are working in the school hall to help with setting up the stage for a play or an assembly. Perhaps you've got a stage that is raised up and there are some steps that lead up to the stage. From the side the steps might look a bit like this:-
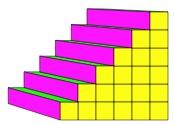
These steps have been made up using blocks so that you go up a total of 6 and along a total of 6. The steps could have been made up another way:-
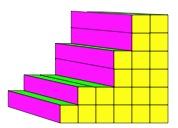
In this case the steps are not equal and some of them need you to make a big step up. Well, that does not matter.
Have a go at drawing some other steps that would take you up 6 and along 6.
My challenge to you today is to design different step arrangements, with the following rules:-
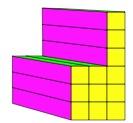
You need to go along a distance of 6 on the steps, so this one breaks the rule:-
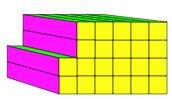
You cannot go DOWN once you have gone up. So this next one is not allowed either:-
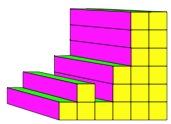
But, you can go along more than one block without going UP like this one:-
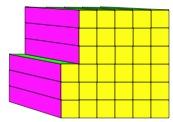
As a little extra, you may have noticed that you can count how many square blocks have been used for each design.
The very first example above used 21 and the last one used 33 square blocks.
Here are some questions you might like to think about to do with the number of square blocks used:-
- What is the largest number of square blocks that can be used?
- What is the smallest number of square blocks that can be used?
- Can you get to use all the numbers that go between your answer to a. and your answer to b. ?
I wonder what would happen if it were 4 along and 4 up?
I wonder what would happen if it were 5 along and 5 up?
I wonder what would happen if it were 5 along and 6 up?
I wonder what would happen if it were 6 along and 5 up?
I wonder what would happen if ...?
Please send in your solutions and comments.
Getting Started
Trying out the stairs using blocks, or drawing them on squared paper, will help.
What will the last block have to look like?
What might the first block look like?
Student Solutions
Here is a solution to STAIRS, which we very happily received from Hannah of West Flegg Middle School, Norfolk. She writes:
| 1. Image

|
2. Image

|
3. Image

|
4. Image

|
| 5. Image

|
6. Image

|
7. Image

|
8. Image

|
| 9. Image

|
10. Image

|
11. Image

|
12. Image

|
| 13. Image

|
14. Image

|
15. Image

|
16. Image

|
| 17. Image

|
18. Image

|
19. Image

|
20. Image

|
Biggest and smallest:-
This is my biggest

This is my smallest

Then:-


14 on the first sheet - No 19.
15 on the sheet - Nos. 14, 2, 3, 6.
16 on the sheet - No. 9.
17 on the sheet - Nos. 8, 13, 18.
18 on the sheet - Nos. 4, 11.
19 on the sheet - Nos. 1, 12, 13, 16.


22 on the sheet - No. 10.
23 on the sheet - No. 17.


And so on... you can just add one to the last square, up the top if you like. I added them up at the top of the last three.
She went on to extend the challenge! WELL DONE
I wonder what would happen if it were 5 along and four up?

The amount would be smaller all the time but the method would be the same.
She also looked at 5 by 6 and 6 by 5. She finishes by saying:
I wonder what would happen if you could have two sets of steps?
e.g.,

Bernard says "Well done, a good approach. I liked the way you had a go, then sorted them into an order, put in the missing ones, and saw how it was just going to go on. Then you asked a further question, and explored it a little. And you finished with a brand new question. Keep up this good work all of you!''
