Snapped Palm Tree
A palm tree has snapped in a storm. What is the height of the piece that is still standing?
Problem
A palm tree that was 16 metres tall has snapped in a storm, so that the top of the palm tree has landed 8 metres from the base.
What is the height of the piece of the trunk that is still standing (vertically)?
Image
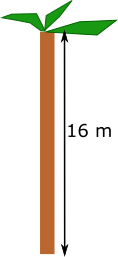
Image

This problem is adapted from the World Mathematics Championships
Student Solutions
Labelling the two parts of the trunk
Suppose the vertical part of the trunk is $a$ and the slanted part is $b$, where $a$ and $b$ are in metres, as shown below.
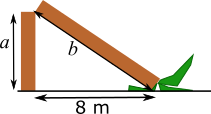
Then $a+b=16$, and $a$, $b$ and 8 are the sides of a right-angled triangle with hypotenuse $b$, so $a^2+8^2=b^2$.
This gives us the simultaneous equations $a+b=16$ and $a^2+64=b^2$.
Solving by substitution of $b$
Since we want $a$, it is sensible to make $b$ the subject of one of the equations and then substitute that into the other one.
$a+b=16$, so $b=16-a$.
Substituting that into the other equation gives $$\begin{align}a^2+64&=\left(16-a\right)^2\\
a^2+64&=256-32a+a^2\\
64&=256-32a\\
32a&=256-64\\
32a&=192\\
a&=6\end{align}$$
So the height of the part of the trunk that is still standing is 6 metres.
Solving by substitution of $b^2$
Since we want $a$, it is sensible to use substitution to remove $b$ from the equations. As $b^2$ is already the subject of the second equation, we could also make $b^2$ the subject of the first equation, and then equate them.
$$\begin{align}a+b&=16\\
b&=16-a\\
b^2&=\left(16-a\right)^2\\
b^2&=256-32a+a^2\end{align}$$
But from the second equation, $b^2=a^2+64$, so
$$\begin{align}a^2+64&=256-32a+a^2\\
64&=256-32a\\
32a&=256-64\\
32a&=192\\
a&=6\end{align}$$
So the height of the part of the trunk that is still standing is 6 metres.
Labelling the parts of the trunk in terms of the height
The total length of the trunk of the palm tree was 16 metres, so if the height of the part that is still standing is $h$, where $h$ is in metres, then the slanted section must be 16$-h$. This is labelled in the diagram below.
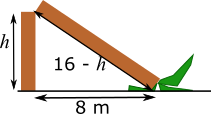
The three lengths labelled in the diagram form a right-angled triangle with hypotenuse $16-h$, so $h^2+8^2=\left(16-h\right)^2$ by Pythagoras.
Solving for $h$,
$$\begin{align}h^2+8^2&=\left(16-h\right)^2\\
h^2+64&=256-32h+h^2\\
64&=256-32h\\
32h&=256-64\\
32h&=192\\
h&=6\end{align}$$
So the height of the part of the trunk that is still standing is 6 metres.
Suppose the vertical part of the trunk is $a$ and the slanted part is $b$, where $a$ and $b$ are in metres, as shown below.
Image

Then $a+b=16$, and $a$, $b$ and 8 are the sides of a right-angled triangle with hypotenuse $b$, so $a^2+8^2=b^2$.
This gives us the simultaneous equations $a+b=16$ and $a^2+64=b^2$.
Solving by substitution of $b$
Since we want $a$, it is sensible to make $b$ the subject of one of the equations and then substitute that into the other one.
$a+b=16$, so $b=16-a$.
Substituting that into the other equation gives $$\begin{align}a^2+64&=\left(16-a\right)^2\\
a^2+64&=256-32a+a^2\\
64&=256-32a\\
32a&=256-64\\
32a&=192\\
a&=6\end{align}$$
So the height of the part of the trunk that is still standing is 6 metres.
Solving by substitution of $b^2$
Since we want $a$, it is sensible to use substitution to remove $b$ from the equations. As $b^2$ is already the subject of the second equation, we could also make $b^2$ the subject of the first equation, and then equate them.
$$\begin{align}a+b&=16\\
b&=16-a\\
b^2&=\left(16-a\right)^2\\
b^2&=256-32a+a^2\end{align}$$
But from the second equation, $b^2=a^2+64$, so
$$\begin{align}a^2+64&=256-32a+a^2\\
64&=256-32a\\
32a&=256-64\\
32a&=192\\
a&=6\end{align}$$
So the height of the part of the trunk that is still standing is 6 metres.
Labelling the parts of the trunk in terms of the height
The total length of the trunk of the palm tree was 16 metres, so if the height of the part that is still standing is $h$, where $h$ is in metres, then the slanted section must be 16$-h$. This is labelled in the diagram below.
Image

The three lengths labelled in the diagram form a right-angled triangle with hypotenuse $16-h$, so $h^2+8^2=\left(16-h\right)^2$ by Pythagoras.
Solving for $h$,
$$\begin{align}h^2+8^2&=\left(16-h\right)^2\\
h^2+64&=256-32h+h^2\\
64&=256-32h\\
32h&=256-64\\
32h&=192\\
h&=6\end{align}$$
So the height of the part of the trunk that is still standing is 6 metres.
