Slippage

It is often too easy to dive into algebra or trigonometry to solve problems when other routes to solutions are available, especially when the question says "find" rather than "calculate". The two solutions below, one from Richard and one from Andrei take different approaches. We also solved this using dynamic geometry software.

Peter of Richard Hale School, approached the problem using trial and improvement. Here is his solution:

My method of trial and improvement for this problem was to pick an angle to the horizontal, consider a ladder placed at that angle and make it touch the ground, the wall and the corner of the storage box. I then calculated the length of that ladder. I then altered the angle until the length of the ladder was $3$ metres. I then used the angle to calculate the height at which the ladder touched the wall. \par This can be done by applying $\sin$ and, $\cos $ in the two right-angled triangles formed between the box, the ladder, the ground and the wall. \par Once I knew the angle at which the ladder would be $3$m long, I could apply $\sin$ in the large right-angled triangle to find the height against the wall.

Image

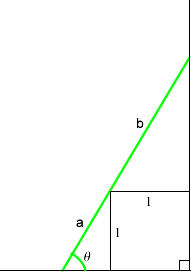
In the lower triangle, if we specify an angle to the horizontal $$\theta$ and use the $1$m side of the block as a side of the triangle, we can work out the hypotenuse

$$a= \frac{1}{\sin \theta}$$

For the top triangle, the hypotenuse is given by $$b= \frac{1}{\cos \theta}$$. In both cases $1$ is the length of the side of the box. Therefore it is possible to create one formula that can be used to easily calculate the length of the ladder from any angle to the horizontal specified. That formula, with distance as $s$ and the angle to the horizontal as theta, is:

$$s = \frac{1}{\sin \theta} + \frac{1}{\cos \theta}$$

Before doing my trial and improvement, I attempted to rearrange the equation to make theta the subject. I was not able to do this, and so went ahead with my trial and improvement approach. I started with $45$ degrees, which produced a ladder length of $2.828$ metres. I tried the following angles, which produced the lengths shown:

50 degrees - 2.861m

60 degrees - 3.155m

55 degrees - 2.964m

56 degrees - 2.995m

57 degrees - 3.028m

56.5 degrees - 3.011m

56.25 degrees - 3.003m

56.2 degrees - 3.001m

At that point I decided that the number of decimal places was enough, and that because I could not solve the equation for the right variable, it would take too long to reach the answer exactly by trial and improvement. Therefore, the ladder is placed at 56.2 degrees to the horizontal, and, using $\sin$ ratio in the larger triangel I obtained:

$$h = 3\times \sin 56.2^\circ = 2.493\mbox{m}$$

On the other hand Andrei of Tudor Vianu College took an algebraic approach. Andrei ended with a quartic and offers three solutions. There is quite a jump from the ratio formula to the three solutions but the first part is very useful.

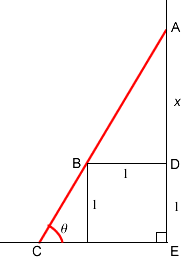
This way the similarity ratio of the upper triangle and the whole triangle is:

$$\frac{AB}{AC}=\frac{AD}{AE}$$

Which gives:

$$ \frac{\sqrt{x^2+1}}{3}= \frac{x}{x+1}$$

This could be treated as an equation in $x$. Evidently, $x$ must be positive ( being a length) and smaller than $2$ (the leg of any right angled triangle must be smaller than the hypotenuses), i.e. $x + 1 < 3$.

The equation above has three solutions for $x$:

\begin{eqnarray} x_1 &=& -\frac{1}{2}+\sqrt{\frac{5}{2}}-\frac{1}{2}\sqrt{7-\sqrt{10}} &\cong 0.6702\\ x_2 &=& -\frac{1}{2}+\sqrt{\frac{5}{2}}+\frac{1}{2}\sqrt{7-\sqrt{10}} &\cong 1.4921\\ x_3 &=& -\frac{1}{2}-\sqrt{\frac{5}{2}}-\frac{1}{2}\sqrt{7-\sqrt{10}} &\cong -3.9062 \end{eqnarray} and solution no. $3$ is not a solution for the geometry problem.

Now, from the first two solutions, the second is to be chosen, being greater, and the height corresponding to it is $x + 1 = 2.49$ m, this being the maximum height.

It seems surprising that there are only two solutions where the ladder touches the obstacle, the ground and the wall.