Slide Height
How high is the top of the slide?
Problem
The ladder to a slide is 5 metres long, and the slide is 12 metres long. The ladder meets the slide at a right angle. This is shown in the diagram.
The distance along the ground from the bottom of the ladder to the bottom of the slide is 13 metres, as shown in the diagram.
How high off the ground is the top of the slide, to the nearest centimetre?
Image
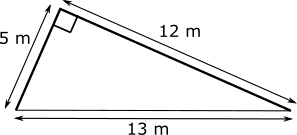
This problem is adapted from the World Mathematics Championships
Student Solutions
Using area
On this diagram, the height we are looking for is labelled $x$ m.
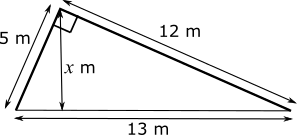
There are two ways to view area of the triangle. One is that it has a base of 12 and perpendicular height of 5, and so its area is $\frac{1}{2}\times5\times12 =30$m$^2$.
The other way we can view it is with a base of 13 and perpendicular height of $x$ and so it also has area $\frac{1}{2}\times13x$. We can equate these two areas to get that:
$\frac{13}{2}x = 30 \Rightarrow x=\frac{30\times2}{13}=4.62$m to the nearest cm
Using similar triangles
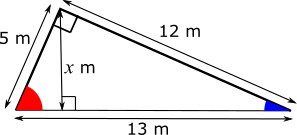
The height must make a right angle with the ground, which is shown in the diagram below. Also on the diagram, the red angle, the blue angle and a right angle must add up to 180$^{\text{o}}$, because the angles in a triangle add up to 180$^{\text{o}}$, and they are the angles in the triangle made by the slide and the ground.
The triangle outlined in gold in the diagram below is also a right-angled triangle. It contains the blue angle and a right angle, so, to add up to 180$^{\text{o}}$, the third angle must be the same as the red angle.
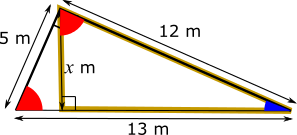
This means that the triangle made by the slide and the ground must be similar to the golden triangle.
The hypotenuse of the triangle made by the slide and the ground is 13 m, and the hypotenuse of the golden triangle is 12 m. So the sale factor between the two triangles is $\frac{12}{13}$.
The height, $x$ m, corresponds to the 5 m side of the larger triangle (the ladder). So the height is $\dfrac{12}{13}$ of 5, which is 4.61538..., which is 4.62 m to the nearest cm.
On this diagram, the height we are looking for is labelled $x$ m.
Image

There are two ways to view area of the triangle. One is that it has a base of 12 and perpendicular height of 5, and so its area is $\frac{1}{2}\times5\times12 =30$m$^2$.
The other way we can view it is with a base of 13 and perpendicular height of $x$ and so it also has area $\frac{1}{2}\times13x$. We can equate these two areas to get that:
$\frac{13}{2}x = 30 \Rightarrow x=\frac{30\times2}{13}=4.62$m to the nearest cm
Using similar triangles
The height must make a right angle with the ground, which is shown in the diagram below. Also on the diagram, the red angle, the blue angle and a right angle must add up to 180$^{\text{o}}$, because the angles in a triangle add up to 180$^{\text{o}}$, and they are the angles in the triangle made by the slide and the ground.
Image

The triangle outlined in gold in the diagram below is also a right-angled triangle. It contains the blue angle and a right angle, so, to add up to 180$^{\text{o}}$, the third angle must be the same as the red angle.
Image

This means that the triangle made by the slide and the ground must be similar to the golden triangle.
The hypotenuse of the triangle made by the slide and the ground is 13 m, and the hypotenuse of the golden triangle is 12 m. So the sale factor between the two triangles is $\frac{12}{13}$.
The height, $x$ m, corresponds to the 5 m side of the larger triangle (the ladder). So the height is $\dfrac{12}{13}$ of 5, which is 4.61538..., which is 4.62 m to the nearest cm.
