Order the products

Answer: 

186$\times$214 (smallest)

210$\times$190

195$\times$205

198$\times$202

200$\times$200 (largest)

Numerically, using 200$\times$200

210$\times$190 = (200 + 10)(200 $-$ 10) = 200$^2$ + 2000 $-$ 2000 $-$ 100

                                                    = 200$^2-$ 100

195$\times$205 = (200 $-$ 5)(200 + 5) = 200$^2$ $-$ 1000 + 1000 $-$ 25

                                                = 200$^2-$ 25

198$\times$202 = (200 + 2)(200 $-$ 2) = 200$^2-$ 4

186$\times$214 = (200 + 14)(200 $-$ 14) = 200$^2-$ 14$^2$

$\therefore$ 186$\times$214 $\lt$ 210$\times$190 $\lt$ 195$\times$205 $\lt$ 198$\times$202 $\lt$ 200$\times$200 

Writing the numbers in terms of 200

All of the products are $(200 +n)(200 -n)$ for some small value of $n$.

$\begin{align}(200+n)(200-n)&=200^2+200n-200n-n^2\\

&=200^2-n^2\end{align}$

$n$ larger $\Rightarrow200^2-n^2$ smaller (for $n\gt0$).

$\therefore$ 186$\times$214 $\lt$ 210$\times$190 $\lt$ 195$\times$205 $\lt$ 198$\times$202 $\lt$ 200$\times$200

Diagrammatic representation

Red strip and green strip both have width $1$, area $200$

Image

 

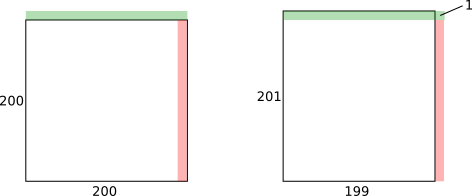
Red strip and green strip both have width $n$, area $200n$

Image