Next-door Numbers
Problem
Florence chooses a number and then counts on one more:
She adds them together and this is what she records: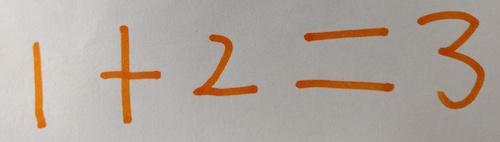
Ethan chooses two different 'next-door' numbers: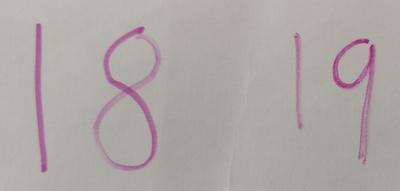
And then he adds them together and records the addition: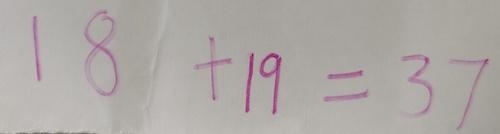
Here are the 'next-door' (consecutive) numbers that Alma chooses:
She adds her numbers together: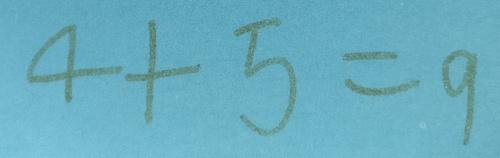
Try this for yourself. Choose two consecutive numbers and add them together.
What is the same about all the answers?
Does this surprise you?
Will this always happen when you add two consecutive numbers together?
Try drawing a picture or making a model to explain your thinking.
Can you convince someome else using your picture/model?
You may be interested in the other problems in our Surprise! Feature.
Getting Started
Can you find two next-door numbers that add to 6? Or 10?
Student Solutions
Well done to everybody who worked out that the answer will always be odd!
Liam from England said:
When you add 2 numbers next to each other their answer will always be an odd number because 15 is an odd number and 16 is an even number they will always add up to become an odd number.
Ariana from Halstead Preparatory School in the UK agreed with Liam:
There are odd numbers when you add next door neighbour numbers because odd plus even equals odd.
Well done to both of you - an odd number plus an even number does equal an odd number! I wonder why next-door numbers always have one odd number and one even number? And I wonder why adding an odd number and an even number makes an odd number?
The next few solutions are also from children at Halstead Preparatory School.
Juliet drew a picture using Numicon shapes to represent the two numbers she was adding:
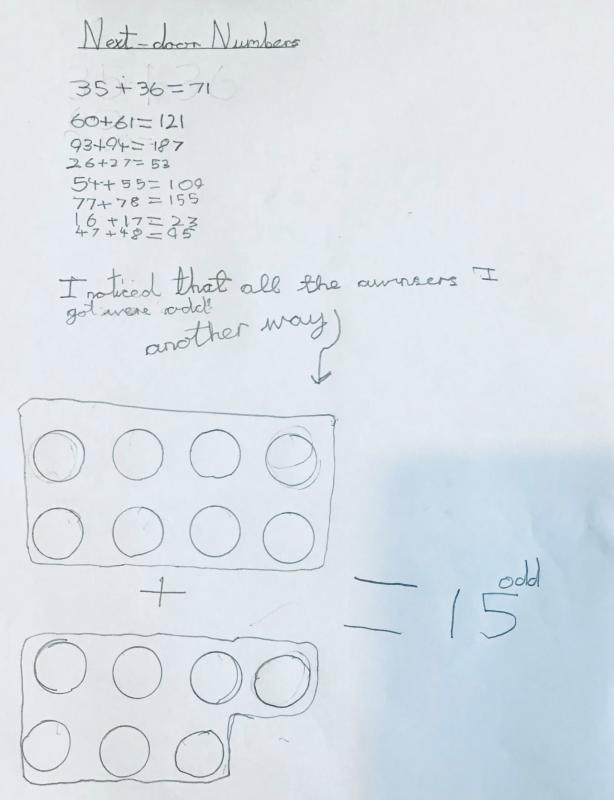
Good idea, Juliet! Can you try representing some other pairs of next-door numbers with Numicon shapes? What do you notice?
Mia drew similar shapes to represent adding 3 and 4:
Well done, Mia! I wonder if we can tell from that picture that 3 is an odd number and 4 is an even number?
Lika used these pictures to represent adding two next-door numbers, where one number has been drawn as red squares and the other number has been drawn as green squares:
This is a good way of representing those numbers, Lika! What do you notice about each picture? Why does this show that the sum of two next-door numbers will be odd?
D from Crossflatts in the UK sent in this explanation:
I noticed that with any next-door numbers, that one number will always be odd and the other will be even.
If I add two numbers that are the same size together, then the answer is always even. So if I add one number that is odd and another that is even, then I always get an odd number.
Well done, D! I wonder why adding a number to itself always makes an even number?
Viren KS sent in an explanation for why the sum will always be odd using algebra to represent the two next-door numbers. If you have met algebra before, then you might like to take a look. Or you may be curious to look anyway! Click 'show' below to see Viren's explanation.
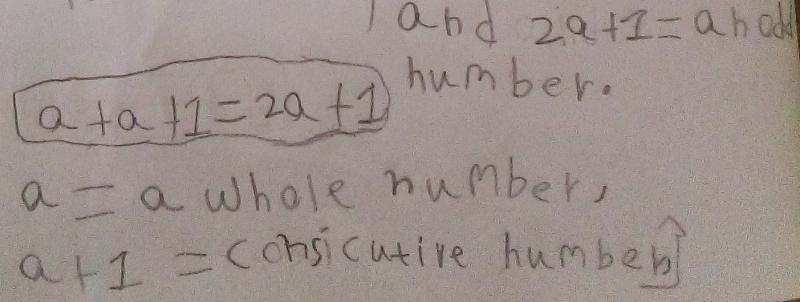
Well done, Viren! Viren has represented a number with the letter 'a', and then the next number will be one more, or 'a + 1'. When we add these together we get a + a + 1, which we can write as 2a + 1. This is an odd number because 2a is in the two-times table, so it is an even number, which means when we add one more we will get an odd number.
Thank you to everybody else who sent in their ideas - we also had excellent solutions sent in by Elena and Eva at Halstead Preparatory School.
Teachers' Resources
Next-door Numbers
Florence chooses a number and then counts on one more:
She adds them together and this is what she records:
Ethan chooses two different 'next-door' numbers:
And then he adds them together and records the addition:
Here are the 'next-door' (consecutive) numbers that Alma chooses:
She adds her numbers together:
Try this for yourself. Choose two consecutive numbers and add them together.
What is the same about all the answers?
Does this surprise you?
Will this always happen when you add two consecutive numbers together?
Try drawing a picture or making a model to explain your thinking.
Can you convince someome else using your picture/model?
Why do this problem?
This problem is aimed at young children who are becoming familiar with the concept of odd and even numbers. The outcome (that any two consecutive numbers add to make an odd number) may seem obvious to us, but it is likely to come as a surprise to learners. The fact that this always happens is unexpected and hooks them in, providing a motivating context in which
children can deepen their understanding of our number system and create proofs.
Possible approach
Ask everyone to think of two 'next-door' (consecutive) numbers and to add them together. You could suggest that everyone checks their answers with a partner then invite learners to call them out and write them on the board. What is the same about all these numbers? If they do not mention that all the numbers are odd, you could mark the answers on a number line, which might help.
Listen and watch out for children who seem surprised by the fact the answer is always odd. Can they explain why they are surprised?
Challenge the class to work in pairs to investigate whether this always happens when you add two consecutive numbers together. If any pair thinks they have found an even total, you could ask them to check with another pair.
Try not to steer them in the direction of particular equipment when you invite them to draw a picture or make a model to explain their thinking. However, if some are really stuck, you could give them a range of classroom resources (e.g. squared paper, Numicon, Multilink...) so they still need to choose which they might use.
Key questions
What is the same about all these numbers?
Will you always get an odd number when you add two consecutive numbers together?
How do you know?
You could choose some equipment to help you make a model or draw a picture.
Possible support
Offering a limited range of equipment, as suggested above, will help some children.
Possible extension
The problem Two Numbers Under the Microscope, which focuses on adding two odd numbers together, would make a good follow-up task at a later stage.