Networks and Nodes
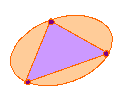
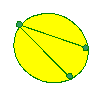
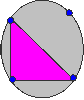
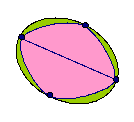
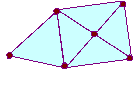
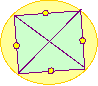
Without taking your pencil off the paper or going over a line or
passing through one of the points twice, can you follow each of the
networks?
Problem
Image
|
Image
|
Image
|
Image

|
Without taking your pencil off the paper or going over a line
or passing through one of the points twice, can you follow each of
the networks?
If you are able to do this, mark your pathway and direction using arrows. Create your own networks. Can you draw one that is impossible to complete without lifting your pencil? |
Image
|
Image

|
Image
|
Image
|
Getting Started
Try marking the nodes you pass through which are not the start or
end points.
Do you notice anything about them?
Do you notice anything about them?
Student Solutions
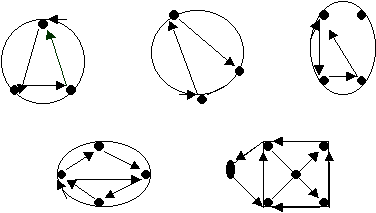
Could you draw the shapes without removing your pencil from the paper. Which ones were possible and which ones impossible?
These are the networks that Mithran, who is from Australia, could follow. He has sent in his results and shown with arrows the path that he took in completing the shapes. Try some for yourself.
Image
Teachers' Resources
Why do this problem?
This problem makes a good whole class activity as it is suitable for all attainment levels but includes an element of logical thinking to challenge the highest attainers. It fits within the topic of topology which is not strictly within the curriulum but has lots of links to the language of shape and
space.
Possible approach
Ask a child to come to the board/whiteboard and draw a simple line picture or design without taking their pen off the surface. Change the colour of the pen and ask another child to come and copy, or go over, what the first child did. Ask a few simple questions such as "How did they know where to start?", "Did they remember or was there a clue in the way it was drawn?", "Would it work
starting at a different place (node)?".
Give the children a little time to work in pairs doing the same activity - one draws a network and the other has to find a route through it without taking their pen off the paper. Again, different coloured pens are helpful. Ask them the same sorts of questions to draw out any method they have found.
Offer the networks in the problem (you could print off this sheet of the diagrams) and ask the children to work by themselves or in pairs to find a unicursal (continuous) route for each one. Challenge them to find more than one route, marking each with arrows as indicated in the problem and showing at which node they started.
Now offer the challenge - can they draw a network that cannot be traced in one go? If they think they have, suggest that they draw it and post it somewhere central for others in the class to take up the challenge. That may be enough activity for most of the class, but the key questions to ask those who want to take it further are:
Is there a way of telling which networks can, and which can't, be traced?
Is there a way to tell which node is a starting node?
Key questions
If we can do it, does it matter where we start?
Is there a node we can start at that won't work?
How do you know?
Possible extension
Is there a way of telling which networks can, and which can't, be traced? Is there a way to tell which node is a starting node? Listen for explanations which describe going in and out of nodes. You might want to offer the well known The Bridges of Konigsberg problem as a further extension..
Possible support
All children will be able to try these activities. For those children who do need support, indicate the starting place.
