Missing 9s
Sara makes a list of the whole numbers that do not contain any 9s. What is the 300th number on her list?
Problem
Sara makes a list of the whole numbers in ascending order which do not have 9s as any of their digits.
1 is the first number on Sara's list.
What is the 300th number on Sara's list?
This problem is adapted from the World Mathematics Championships
Student Solutions
Answer: 363
Counting 300 places on Sara's list
Between 1 and 100, Sara won't list 9, 19, 29, 39, 49, 59, 69, 79, 89 or 90 - 99.
19 numbers will be missed between 1 and 100, 81 will be listed
100 will be the 81st number
81 numbers will be listed between 101 and 200
200 will be the 162nd number
81 numbers will be listed between 201 and 300
300 will be the 243rd number
301 will be the 244th number
...
308 will be the 251st number
310 will be the 252nd number
...
318 will be the 260th number
320 will be the 261st number
...
328 will be the 269th number
330 will be the 270th number
...
340 will be the 279th number
...
350 will be the 288th number
...
360 will be the 297th number
...
363 will be the 300th number
Counting in blocks with a diagram
Image
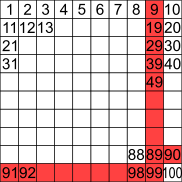
Representing the numbers 1 to 100 in a square, the numbers Sara won't list are shown in red.
Image

The numbers up to 100 on Sara's list make a 9 by 9 square.
81 numbers in this square
Image
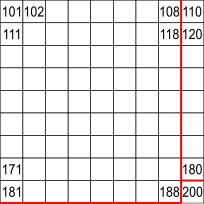
The square from 101 to 200 is similar
81 numbers in this square makes 162 altogether
Image
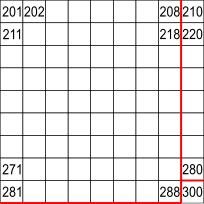
The square from 201 to 300 is similar
81 numbers in this square makes 243 altogether
57 more numbers to reach 300
Image
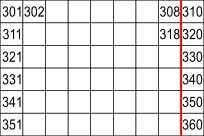
Rows from the square from 301 to 400
The rows are all 9 numbers long
9$\times$6 = 54 numbers in this block
3 more numbers to reach 300
Image
300th number is 363
Using base 9
Numbers written in base 9 do not contain any 9s.
In base 9, the numbers 1, 2, 3, 4, 5, 6, 7, 8 are written as usual, but the number '9' is written as 10. Instead of having a ones column and a tens column and a hundreds (=10$^2$) column and so on, base 9 has a ones column and a nines column and an eighty-ones (=9$^2$) column and so on. For example, '18' is written as 20 because it is 2 nines and 0 ones, and '82' is written as 101 because it is 1 eighty-one, 0 nines and 1 one.
To find the 300th number on Sara's list, write 300 in base 9.
3$\times$81 = 243 < 300
4$\times$81 = 324 > 300
There are 3 eighty-ones in 300, remainder 57.
57 = 6$\times$9 + 3,
So 300 = 3$\times$81 + 6$\times$9 + 3
In base 9 it is written 363.
