Magic 7
Can you complete this magic square with the numbers from 7 to 15?
Age
11 to 14
Challenge level
Problem
Image
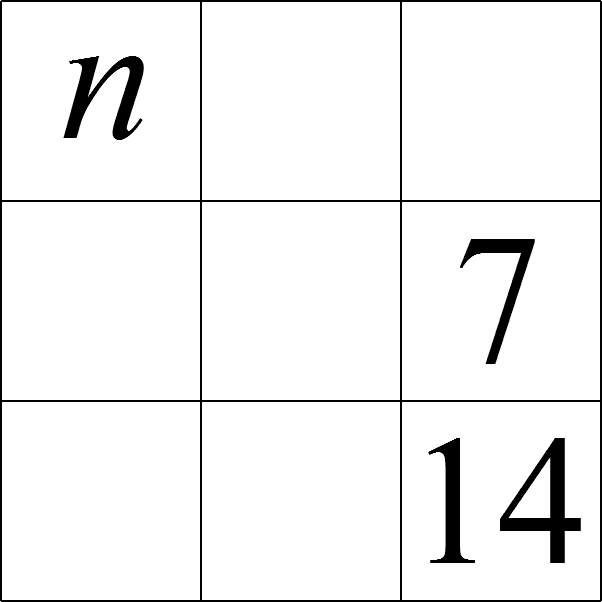
In this magic square, which uses all the integers from $7$ to $15$, each of the rows, columns and the two main diagonals has the same total.
Which number replaces $n$ in the completed square?
If you liked this problem, here is an NRICH task that challenges you to use similar mathematical ideas.
Student Solutions
Answer: 8
7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 = 99 = sum of all 3 rows
$\therefore$ sum of each row is 33
Writing the numbers in terms of $n$
Image
Image
Image
Image
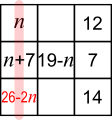
Image
$\begin{align}26-2n\ \ +\ \ 19-n\ \ +\ \ 12\ \ &=33\\
26+19 + 12-33&=3n\\
24&=3n\\
8&=n\end{align}$
Writing the numbers in terms of $x$
Image
Image
Say $n$ + 12 + $x$ + 12 = 33,
then $n$ + 14 + ($x-$2) = 33
Image
Same idea gives $x-$4 at the bottom
$\therefore$ 3$x$-6=33, so $x$ = 13
And $n$ + $x$ + 12 = 33 $\Rightarrow n$ + 13 + 12 = 33 $\Rightarrow n$ = 8
Using reasoning and not algebra
Image
Image
33 $-$ 14 = 19
19 = 7 + 12
19 = 8 + 11
19 = 9 + 10
no more options so these 4 numbers are 8, 9, 10, 11
Image
$n$ + middle + 14 = bottom + middle + 12
difference between $n$ and bottom = difference between 12 and 14
This gives 2 options:
Image
Image
