Lawn border
Problem
I was trying to imagine what my lawn would look like with a nice paved border around it. So I used some tiles that were all the same size but different colours, to build a little model. This is how it looked:
Make some kind of model or picture of your own that shows the same sizes.
Look at the number of tiles for different parts.
I wondered what my border would be like if I changed some of the tiles. I made it like this:
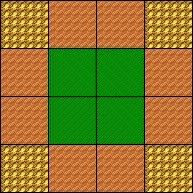
What do you notice has changed?
I decided I'd make some more changes to my model garden. I did this.
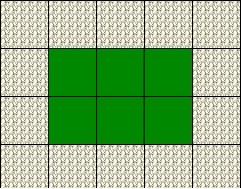
How does this compare with the last one?
I made one last model with some different tiles. Here it is. I liked this one.
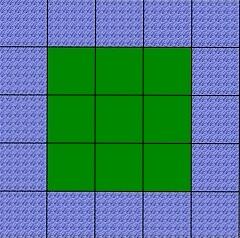
Have a good look now at the numbers of the different tiles in different places for each of my models.
If I use $12$ tiles to make a lawn, how many tiles would I need to make a border?
How many differently shaped lawns can you make with $12$ tiles?
Do you need a different number of border tiles to go around each lawn shape?
Can you make models to show what the different gardens would look like?
Getting Started
How many along the length of each lawn?
How many in total are needed for the lawn?
How many tiles are there along the width of the border?
How many along the length of the border?
How many tiles in total are needed for the border?
Can you predict the number of border tiles that would be needed for a differently shaped lawn?
How did you know?
Student Solutions
Rosie from the Thomas Deacon Academy in Peterborough U.K. sent in the following accompanied by the diagrams.
From carrying out this solution, I have found that the more corners there are to the shape of the lawn the more tiles you need, as for every corner you need an extra tile to go in the tip (edge). I found many differant shapes that could be used for the lawn and tiles and have included the most interesting and practical ones.
Finlay from Sutton in the U.K. said the following:
The solution to a rectangular lawn is:
Mathematical terms:$(n x 2) + (X x 2) + 4$
English terms: if you multiply on side of the lawn by two and add it to a different length side multiplied by two, and then add four it will equal the number of tiles around the lawn.
Thank you, both of you for these good solutions.
Teachers' Resources
Lawn Border
I was trying to imagine what my lawn would look like with a nice paved border around it. So I used some tiles that were all the same size but different colours, to build a little model. This is how it looked:
Make some kind of model or picture of your own that shows the same sizes.
Look at the number of tiles for different parts.
I wondered what my border would be like if I changed some of the tiles. I made it like this:
What do you notice has changed?
I decided I'd make some more changes to my model garden. I did this.
How does this compare with the last one?
I made one last model with some different tiles. Here it is. I liked this one.
Have a good look now at the numbers of the different tiles in different places for each of my models.
If I use $12$ tiles to make a lawn, how many tiles would I need to make a border?
How many differently shaped lawns can you make with $12$ tiles?
Do you need a different number of border tiles to go around each lawn shape?
Can you make models to show what the different gardens would look like?
Why do this problem?
Possible approach
- the number of tiles along the width of the lawn
- the number of tiles along the length/breadth of the lawn
- the number of tiles needed in total to make the lawn
- the number of tiles along the width of the border
- the number of tiles along the length/breadth of the border
- the number of tiles in total that will be needed to make the border around the lawn.