How far does it move?

Experiment with the interactivity of "rolling" regular polygons, and explore how the different positions of the dot affects the distance it travels at each stage.

Age

11 to 14

Challenge level

Secondary

ALGEBRA

Functions and Graphs

Exploring and noticing Working systematically Conjecturing and generalising Visualising and representing Reasoning, convincing and proving

Being curious Being resourceful Being resilient Being collaborative

Problem

How Far Does it Move? printable sheet

Take a look at the interactivity below which shows regular polygons "rolling" along the horizontal surface.

It leaves a trace of the path of the dot and on the graph it records the distance that the dot travels.

Experiment by positioning the dot at the centre of the polygons, at one of the vertices or at the centre of one of the sides of the polygons and explore how this affects the distance / time graph.

Challenge:

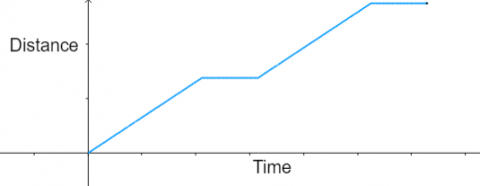
Can you now work out what produced the following distance / time graph?

Can you work out how many sides the polygon had and where the dot was placed?

Try to explain how you worked it out.

Student Solutions

This problem clearly got a lot of you thinking! Several of you sent in the correct answer, including Gemma, Rachel, David, Alex, Charlie, Robert, Joel, Jamie, Carys, Soph, Bex, Rhi, Joe, Veronica, Harriet and Elspeth, all from Cowbridge Comprehensive School.

As Azeem of Mason Middle School states:

You have to have a triangle. Also, you must place the dot at the bottom left corner of the triangle.

Some of you worked it out using some systematic thought and trial and error.

Sathya and Michael made a good effort at explaining how they worked this out .

Sathya from Scots College, New Zealand considered whether or not the dot could be placed in the centre of the shapes:

I first checked whether it could have been the centre of the shapes. This is impossible as it always results in a linear graph.

Sathya then went on to consider how many sides the polygon might have:

Then I checked how many segments in the line and I worked out it was a triangle.

Michael from St John Payne School went a little further in exploring where the dot might be placed:

First I knew it had to be on the vertex because there was a part of the graph that was flat.

The only point at which the dot isn't travelling anywhere when the polygon is rolling is on a vertex, because then the dot is always in contact with the floor.

He then looked at the units on the graph to consider which vertex the point would be on:

This told me the time period for one turn about a vertex, the length of time for which the gradient was zero.

This meant that the polygon had gone through 2 cycles before it was going to pivot on the vertex that held the dot.

This meant that the dot had to be 2 vertices after the bottom right vertex.

This gave enough grounds for trial and error to find the right polygon fairly quickly.

Thank you to Ken Nisbet, the class teacher of 4YP at Madras College in St Andrews, Scotland, for sending us this message and the very impressive work carried out by some of his students:

Hi to 'The Nrich Team'

My 'top' S4 set were this month inspired by your various 'Rolling Polygon' problems.

We decided to investigate the total distance travelled by the dot, when it was placed at one of the vertices, from 'take-off' to 'landing' when each polygon had side length 1 unit.

The class divided into groups of 2 or 3 students. Exact values were the order of the day. The Equilateral triangle and Square were fine though much discussion was needed regarding the final form of the answers. The pentagon proved a lot more challenging with the Golden ratio eventually surfacing.

The overall pattern in the answers were quite remarkable with a very curious sequence emerging:

1, 2, 5, 12, ...

The groups spent over a week working on this investigation with excitement mounting as the sequence developed. Predictions were made at the stage when the hexagon revealed the number 12 as the 4th term. For the Septagon exact values were not possible so conjectures for the 5th term of the sequence were tested using very accurate calculator work (Sine Rule & Cosine Rule etc).

What was a complete surprise was that a non-integral value for the 5th term emerged. There are not many situations, at this level of work, where approximate values can be harnessed to disprove an integer sequence conjecture. "This must be wrong" was the general feeling and all the sums were checked again and again... but eventually calculations by three separate independent groups confirmed the result.

I feel that the challenge and sheer range of technique required for this investigation has benefited my students immensely. They are aged 14 to 15 and produced work of impressive depth and quality. Thanks for the stimulation that your questions have provided ... keep up the great work. I have attached the write-up produced by David, Nicholas and Robert as it was a superb exposition.... I'm sure you will agree!

All the best Ken Nisbet

We do agree! Many thanks.

Teachers' Resources

Why do this problem?

This problem provides a visual context in which to consider how distance / time graphs represent movement over time. It allows opportunities for learners to discuss and refine their ideas. Asking learners to predict, to justify their predictions and to consider modifying their views can help address misconceptions and improve understanding.

Possible approach

With the dot in the centre, ask the group to predict what the path of the dot will be and what the distance-time graph will look like. Learners could sketch the path and graph in advance, before seeing the polygon roll. Their suggestions could be compared and discussed before making a final joint judgement on the shapes of the path and the graph.

Run the interactivity. Discuss how the graphs related to what learners expected. Confirm understanding by asking what would happen if you changed the number of sides of the polygon.

At this point you might choose to do this card sorting activity. Can the students match each polygon to the path traced by its dot and the distance / time graph of the dot's journey?

When the group feel confident, move them on to more challenging situations by moving the dot to a vertex of a pentagon. Ask similar questions about the path of the dot and the distance-time graph.

Allow plenty of time for discussing/comparing different ideas before running the interactivity for the different polygons or point positions. The pause button is useful to focus on the different stages of the journey and to ask for conjectures about what will follow.

Ask pairs or groups to work on new questions, agreeing and drawing the graph and path together before using the interactivity to confirm their ideas.

Suitable questions are:

What happens if the dot is moved to a different vertex?

What happens if the dot is placed on a vertex of a different polygon?

What happens if the dot is in the middle of a side of a polygon?

The challenge set at the end of the problem asks students to identify the polygon and position of the vertex that would produce the given graph. This creates an opportunity for students to work backwards from the graph and consolidate the ideas developed in the previous work. As well as students identifying which polygon and where the dot is, encourage them to articulate why they know this and how they could convince someone else.

Key questions

What does the gradient of the graph relate to?
Why does the dot speed up and slow down at different stages of the "journeys"?
If we change - (the polygon/position of dot) - what will be the same about the graph and what will be different?

Possible support

Spend time on the path of the dot for different polygons and positions so that learners become confident with predicting its locus.

Talk with students about the time the polygon took to turn in one part of its rotation, and how far the dot would travel if placed in various positions for that rotation. Draw conclusions about the speeds it would be travelling, in each of those positions. Talk through speed-while-rotating in relation to radius, give real examples - like being in different positions on a children's roundabout, or attempting to run to keep up with a long rotating arm/beam etc.

Possible extension

Pairs could draw out a distance-time graph they have generated and post it as a challenge for others to establish which initial settings were used (in the least number of guesses).

Imagine a rectangle, a semicircle or some other shape rolling along.

Follow-up problems concentrating on speed-time graphs and $(x,y)$ position against time are Speeding Up, Slowing Down and Up and Across

Or search by topic

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners