Hexagon line
How many hexagons are required for the perimeter of the whole shape to have length 1002cm?
Problem
A shape consisting of a number of regular hexagons is made by continuing the pattern shown in the diagram, with each extra hexagon sharing one side with the preceding one.
Each hexagon has a side length of 1cm.
Image
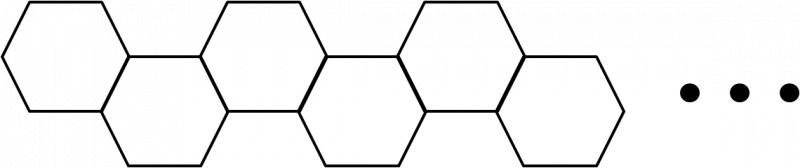
How many hexagons are required for the perimeter of the whole shape to have length 1002cm?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
Answer: 250
The sequence of hexagon lines
Image
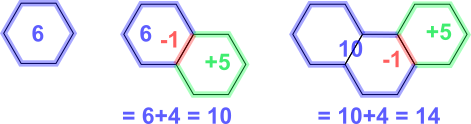
1-hexagon line has perimeter of 6
Each hexagon adds 4 to the perimeter
$\therefore$ perimeter = 6 + 4$\times$ number of hexagons added
So 1002 = 6 + 4$\times$?
$\Rightarrow$ 996 = 4$\times$?
996$\div$4 = 249
The perimeter is 1002 cm when 249 hexagons have been added to the first hexagon, so there are 250 hexagons altogether
Counting the lines in the pattern
Image
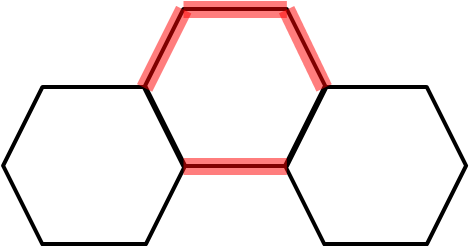
Non-end hexagons contribute 4 cm to perimeter
2 end hexagons contribute 10 cm to the perimeter
$\therefore$ the non-end hexagons contribute 1002$-$10 = 992 cm to the perimeter
992$\div$4 = 248
There are 248 non-end hexagons and 2 end hexagons = 250 hexagons in total
Alternatively, notice that each hexagon contributes $4$cm to the total perimeter, except the end two which contribute $2$ extra cm ($1$cm each), so if we take $2$cm off the total perimeter and divide by $4$ we will have the total number of hexagons in our shape. This gives us $n=250$.
