Gabriel's problem posters
Problem
Student Solutions
Part 1
Part 2
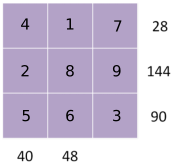
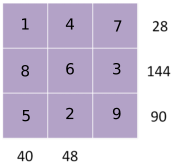
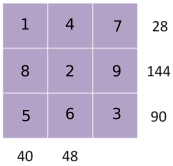
Part 3
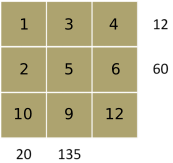
How?
There are many ways, using factors. One method is shown below.
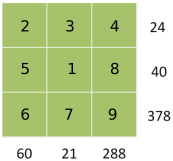
Part 1
378 = 6$\times$7$\times$9 cannot be written as the product of any other 3 numbers under 10
Only 6 is a factor of 60, only 7 is a factor of 21
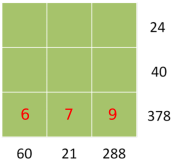
60 = 6$\times$10 so the other two numbers are 2 and 5. 5 is only a factor of 40.
21 = 7$\times$3 so the other two numbers are 3 and 1. 3 is a only factor of 24.
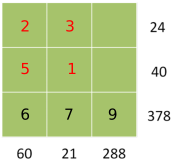
Fill in what is missing to make 24 and 40. We never needed to use the number 288.
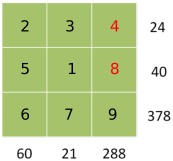
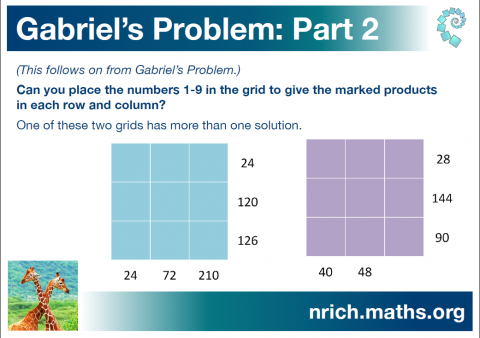
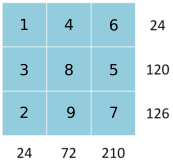
Part 2
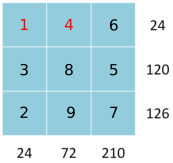
210 = 7$\times$3$\times$10 = 7$\times$3$\times$2$\times$5 = 7$\times$6$\times$5 as the product of 3 numbers less than 10
5 is only a factor of 120 and 7 is only a factor of 126
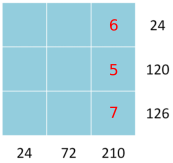
126 = 7$\times$18. 6 already used so 126 = 7$\times$2$\times$9. 9 is only a factor of 72.
120 = 5$\times$24. 6 already used so 120 = 5$\times$3$\times$8. 9 is already in the 72 column, so 3 can't go in there too.
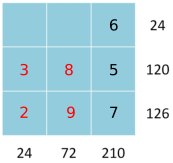
24 = 3$\times$2$\times$4 and 72 = 8$\times$9$\times$1
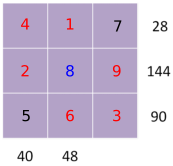
7 is only a factor of 28, 5 is only a factor of 40 and 90
144 = 8$\times$18 and 90 = 5$\times$18
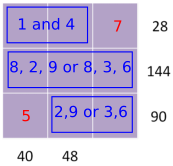
Need to use the 8 for 40 or 48. Try the two options:
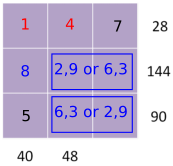
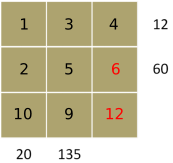
Part 3
135 = 5$\times$27 = 5$\times$3$\times$9 is the only product for 135
9 is not a factor of 12 or 60 and 5 is only a factor of 60
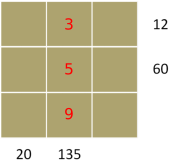
12 = 3$\times$1$\times$4 and 20 = 10$\times$2$\times$1 are the only ways to make 12 and 20, since the 5 is used
12 and 20 both need to use 1
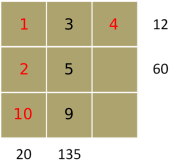
60 = 2$\times$5$\times$6 and so the last number is 12