Equation matcher
Problem
Fitting algebraic curves through experimental data points is an important scientific process which allows us to make predictions of the behaviour of a system away from the observed points. But which equations are sensible choices for a particular set of data? This question draws us into the general process of curve fitting.
In four different sorts of experiments, two values of $x$ and $y$ are successively measured and plotted on charts below: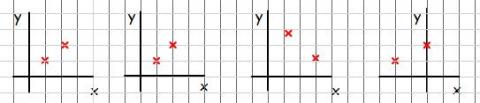
For each chart, which of the following equations are possible descriptions of the underlying process?
$$y = ax+b\quad\quad x = ay + \frac{1}{2} by^2\quad\quad y=\frac{a}{x}$$
$$x=a e^{by}\quad\quad x = \frac{ay}{b+y}\quad\quad x = -a\log_{10}(by)$$
What restrictions would the data place on the ranges of the numbers $a$ and $b$ in each case? For example, do the data points imply that the constants will be positive?
Another point is subsequently measured and plotted on the graphs in each case.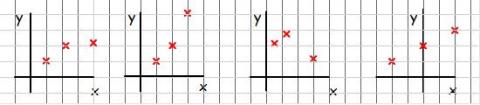
How do the possibilities now change?
Can you give examples of physical systems which are modelled by equations of these types?
Extension: Which curves can be distinguished by three points? i. e., could you pick three points which would rule out all but one of the possibilities in each case?
Teachers' Resources
Why do this problem?
Possible approach
Key questions
- We only have two measurements, but what information can we deduce from these?
- How can we relate this information to the equations?
