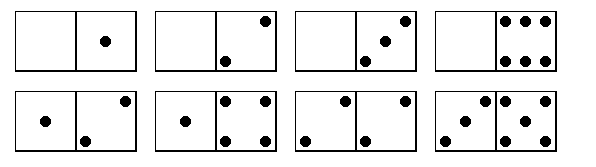
Congratulations to Katherine, from Maidstone Girls' Grammar School who reasoned that there are the 24 unique domino solutions given below, where each arrangement has the 5-3 domino horizontally. Katherine gave the answer 384. She explained that there are 3 columns of dominoes which can be arranged in six different ways. Each of these arrangements can be varied by swopping the rows giving 6 x 4 = 24 arrangements. Katherine then explained that from each of these 24 arrangements you can find 8 others: 4 which are mirror images and 4 which are rotations. This gives 192 (24x8) patterns altogether. Then if you take the 2-2 you can also turn it round 180 degrees to form twice as many solutions. This gives 384 (192x2) domino square solutions.
James of Hethersett High School explained that "I have found that the domino 5-3 is the key domino, as wherever it goes it has to be followed by two blanks." He explained that, from one solution, he found different patterns by swapping the rows or columns. Daniel and Michael of Necton Middle School, Norfolk found one of the solutions. Camilla of Maidstone Girls' Grammar School discovered that in her solutions certain blocks stayed next to one another and concluded that having found one solution all the others are different ways of re-arranging it.
Reflections in the diagonals give patterns with the 5-3 domino placed vertically and reflections in the vertical mirror line give patterns with this domino placed as 3-5. Reflections in the horizontal mirror line turn the vertically placed dominoes upside down.
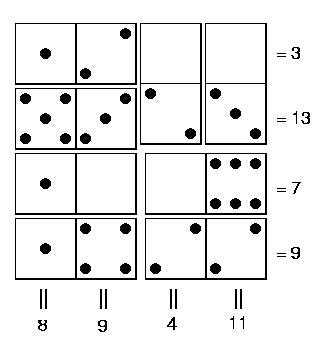
Carrie who goes to Saint Thomas More School has found another solution, based on this pattern of dominoes:
The numbers are:
No-one else has found a different solution that is not derived from the first basic pattern. You may like to investigate patterns such as the one below, or investigate Carrie's pattern further.