Cuisenaire spirals
Can you make arrange Cuisenaire rods so that they make a 'spiral' with right angles at the corners?
Age
7 to 11
Challenge level
Problem
Here are two open spirals made from cuisenaire rods.
Image
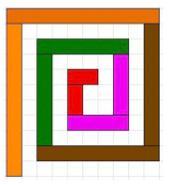
Image
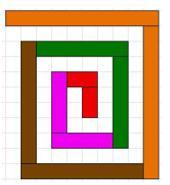
I used only the even numbered rods.
You can experiment making spirals using the rods on our Cuisenaire interactive environment.
There may be some sets of real Cuisenaire rods in your school.
You can experiment making spirals using the rods on our Cuisenaire interactive environment.
There may be some sets of real Cuisenaire rods in your school.
When you've done a lot of exploring you might like to try the something similar with numbers.
If you do, have a look at Number Spirals here.
Getting Started
Perhaps try making a spiral with no gaps first.
Is it possible?
What do you notice about the lengths of the rods?
How are you fitting the rods together each time?
What rules are you following?
Is it possible?
What do you notice about the lengths of the rods?
How are you fitting the rods together each time?
What rules are you following?
Student Solutions
I expect that there were quite a few explorations of these spirals but they did not lead to them being sent in, so remember you can also send in pictures, even if they are on their own!
Erin at North Molton Primary School said:
It doesn't make a difference if you use odd rods or even rods but using them together it doesn't really work as well.
But I'm not to sure what I was supposed to investigate, so that is my solution.
To answer the question about what to investigate it's about seeing what sequences of rods would make a spiral and what kind of rule would that sequence have to have.
From Thomas at C.C.J.S. which I think is Cheltenham College Junior School, we had these thoughts,
If you do your pattern in sets of $2$ then it will end up looking square.
However, if you use a mix of lengths, it will look rectangular
Thank you for those and we hope to hear from you again in future months.
Erin at North Molton Primary School said:
It doesn't make a difference if you use odd rods or even rods but using them together it doesn't really work as well.
But I'm not to sure what I was supposed to investigate, so that is my solution.
To answer the question about what to investigate it's about seeing what sequences of rods would make a spiral and what kind of rule would that sequence have to have.
From Thomas at C.C.J.S. which I think is Cheltenham College Junior School, we had these thoughts,
If you do your pattern in sets of $2$ then it will end up looking square.
However, if you use a mix of lengths, it will look rectangular
Thank you for those and we hope to hear from you again in future months.
Teachers' Resources
Cuisenaire Spirals
Here are two open spirals made from cuisenaire rods.
Image
Image
I used only the even numbered rods.
You can experiment making spirals using the rods on our Cuisenaire interactive environment.
There may be some sets of real Cuisenaire rods in your school.
You can experiment making spirals using the rods on our Cuisenaire interactive environment.
There may be some sets of real Cuisenaire rods in your school.
When you've done a lot of exploring you might like to try the something similar with numbers.
If you do, have a look at Number Spirals here.
Why do this problem?
This exploration provides a good environment for discovery and surprise. There are lots of different ways of exploring the ideas once the main ideas have been grasped. It can develop into a visual pattern spotting exercise as well as a numerical pattern spotting one.
Possible approach
If possible it would be good for all the pupils to see the interactivity and observe closely the gradual formation of the example shown. The activity can then take several different routes according to the questions that are asked.
If there is no access for pupils to use or see the interactivity then using Cuisenaire rods would be best. It would also be possible to create a set of laminated rods in different colours by using this sheet: Word, pdf
If there is no access for pupils to use or see the interactivity then using Cuisenaire rods would be best. It would also be possible to create a set of laminated rods in different colours by using this sheet: Word, pdf
Key questions
What do you notice?
Is there some reason why that happens?
What other groups of rods could you use?
Can you predict the pattern that using different rods produce?
The two shown have a clear pathway in between the rods. It's a spiral too! Could we form a spiral with a sequence of rods that would leave no spaces?
Is there some reason why that happens?
What other groups of rods could you use?
Can you predict the pattern that using different rods produce?
The two shown have a clear pathway in between the rods. It's a spiral too! Could we form a spiral with a sequence of rods that would leave no spaces?
Possible extension
Challenge the pupils to form a spiral in which the lengths of the rods increase in a pattern and they create longer rods to continue it further. Further extension work can be found by moving competent pupils to Number Spirals found here.
Possible support
Pupils will find this task easier if they have access to concrete apparatus.