Cuboid challenge poster
Problem
This poster is based on the problem Cuboid Challenge.
The poster is available as PDF, or the image below can be clicked on to enlarge it.
Student Solutions
The largest volume you can make is when $x = 3\frac13$,
which gives a volume of $592\frac{16}{27}$ cm$^2$.
Why?
For any value of $x$, the other sides are each $20-2x$ and then the volume is $x\times(20-2x)\times(20-2x)$
Trying out values of $x$, a spreadsheet program like Excel is useful
| $x$ | $20-2x$ | volume | $x$ | $20-2x$ | volume | $x$ | $20-2x$ | volume | ||
| 2 | 16 | 512 | 2.5 | 15 | 562.5 | 3.1 | 13.8 | 590.36 | ||
| 3 | 14 | 588 | 3 | 14 | 588 | 3.2 | 13.6 | 591.87 | ||
| 4 | 12 | 576 | 3.5 | 13 | 591.5 | 3.3 | 13.4 | 592.55 | ||
| 5 | 10 | 500 | 3.6 | 12.8 | 589.82 | 3.4 | 13.2 | 592.42 |
You can keep going to get really close to 3.333333...
| $x$ | $20-2x$ | volume | $x$ | $20-2x$ | volume | |
| 3.31 | 13.38 | 592.571 | 3.331 | 13.338 | 592.59237 | |
| 3.32 | 13.36 | 592.585 | 3.332 | 13.336 | 592.59252 | |
| 3.33 | 13.34 | 592.592 | 3.333 | 13.334 | 592.59259 | |
| 3.34 | 13.32 | 592.591 | 3.334 | 13.332 | 592.59257 |
Using a cubic equation, the volume is $x(20-2x)^2$
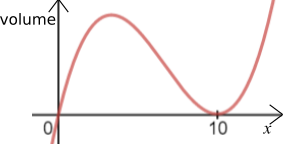
which expands to $4x^3 - 80x^2 + 400x$
Differentiate to find the stationary points:
$\frac{\text{d}V}{\text{d}x} = 12x^2 - 160x + 400$
$\begin{align} 12x^2-160x+400 &= 0\\
\Rightarrow 3x^2 - 40x + 100 &= 0\\
\Rightarrow 3x^2 - 30x -10x + 100 &= 0\\
\Rightarrow 3x(x-10) - 10(x-10)&=0\\
\Rightarrow (3x-10)(x-10)&=0\\
\Rightarrow 3x-10 = 0 \text{ or } x-10 = 0\end{align}$
$x=10$ gives the minimum area of $0$, so $3x=10\Rightarrow x=\frac{10}3$ gives the maximum area.
