Classic Cube
The net of a cube is to be cut from a sheet of card 100 cm square.
What is the maximum volume cube that can be made from a single
piece of card?
Problem
I have a large square piece of card 100cm along each side and have decided to make a large cube from it.
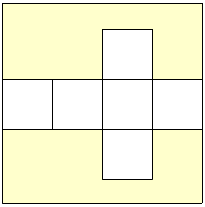
I could cut the net of the cube so that its sides are parallel to the sides of the card and, ignoring any tabs needed to join the edges together, it could look like this:
Image
Image

What is the volume of this cube?
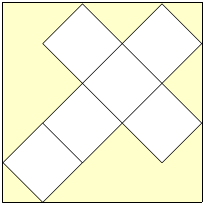
However, I am wasting a lot of the card by cutting the net in this way and I think I can create a cube with a larger volume if I place a net diagonally on the card, like this:
Image
Image

What are the dimensions of the cube with greatest volume I can cut from the card by using different nets and aligning them at an angle to the sides of the card?
Getting Started
Ignore any tabs.
You may like to use a dynamic geometry package or a spreadsheet program to help you. But how will you then convince me that the volume you have found is greatest?
Student Solutions
Image

These solutions came from Fred from Albion Heights Junior Middle School and Low Zhen Lin from Garden International School. Both contributed to this solution. From Low Zhen Lin's diagram you will see that he had the clever idea of cutting one of the faces into four pieces.
To maximize the size of the net, we transform it so that as many of the vertices of the net as possible touch the edge of the paper. This is to maximise the length of the sides and therefore, the volume.
For the traditional net, the most efficient way is to have the lines parallel to the diagonals of the square, as shown in the diagram on the left.
To find the length $E$ of an edge of the cube divide the paper into 5 by 5 and use Pythagoras' theorem. So $E^2 = 20^2 +20^2$ and $E=\sqrt{800}$ or approximately 28.3, and the volume is 22627. Six of the eight non-retroflex vertices touch the edge of the square, and the net fills 48 per cent of the square.
However, this is not the most efficient net. The traditional net has a 3 $\times$ 4 bounding rectangle - the smallest rectangle that it will fit in. The most efficient net will have a bounding rectangle that is a square. That net is shown in the diagram on the right which fills 75 per cent of the square.
The edge of this cube is $\sqrt{1250}$, or approximately 35.4, and the volume is 44194.
Teachers' Resources
Iterative methods or the visual interpretation of graphical solutions are worth exploring. There is lots of room for different approaches, including practical ones, or partly practical and partly analytical.
