Changing Places
Place a red counter in the top left corner of a 4x4 array, which is
covered by 14 other smaller counters, leaving a gap in the bottom
right hand corner (HOME). What is the smallest number of moves it
will take to move the red counter to HOME?
Age
14 to 16
Challenge level
Problem
A four by four square grid contains fifteen counters with the bottom left hand square empty. The counter in the top right hand square is red and the rest are blue. The aim is to slide the red counter from its starting position to the bottom left hand corner in the least number of moves. You may only slide a counter into an empty square by moving it up, down, left or right but not diagonally.
Image
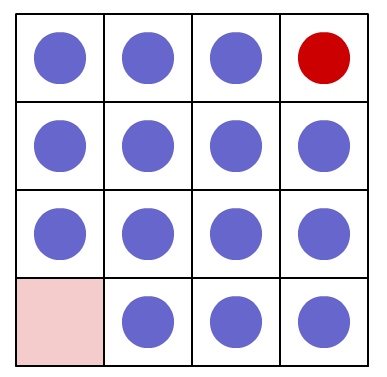
Explore a four by four array. How many moves did you take to move the red counter to HOME (pink square)?
Can you do it in fewer moves? What is the least number of moves you can do it in?
Try a smaller array. How many moves did you take to move the red counter to HOME?
Try a larger array. What is the least number of moves you can do it in?
Have you a strategy for moving down each array?
On which move does the red counter make its first move?
On which moves does the red counter make its other moves?
Can you predict the number of moves that the red counter makes on the way HOME?
Why is the least number of moves ALWAYS odd?
Can you predict what the least number of moves will be for any square array?
Can you explain why YOUR rule works?
You can take this further by considering similar ideas using rectangular arrays or in three dimensions.
Getting Started
Once started on the journey home why is every third move important?
What is special about those counters that don't move?
Student Solutions
We had a number of partial solutions,
including some from The Mount School in York. The two correct
solutions which were sent in from David of the Wreake School and
Andrei of Tudor Vianu National College have been used as the basis
of what is below. Well done David and Andrei. It looks as if the
animation helped to see what was going on and to develop a strategy
that could then be represented in algebraic form.
For a 4x4 array, it was possible to complete the change in 21
moves, which the animation said was the minimum.Trying for grids
from 2x2 to 5x5, the results are written in the following
table:
| Array | Moves |
| 2x2 | 5 |
| 3x3 | 13 |
| 4x4 | 21 |
| 5x5 |
29
|
It is clear that the difference in the number of moves is
always 8.
Now, to predict the necessary number of moves.
Let's imagine the square grid of side n. As 5 is the starting
number, and 8 is taken (n-2) times, we obtain:
5 + 8(n-2) = 8n -16 + 5 = 8n- 11
That is for a grid of size n x n the number of moves seems to
be from the pattern 8n-1.
However, to prove this general formula,we need to analyse the
moves: a) the blue counters from the figure below:
Image
The sketch is done for a 4 x 4 array, but
it could be generalised for an n x n array.
To make the first space for the red
counter we need to create a space below it. This requires you to
move the counters (coloured yellow here) along the last row and
down the last column.
In an n x n array, there are blue counters on every place of
two sides, except the ends, and one in the place of intersection of
the two sides.
So, in total there are: 2(n- 2) + 1 = 2n-
4 + 1 = 2n -3 blue counters needing that number of moves.
b) Now the red counter can move one place down:
Image
c) there is a series of repeated moves from now on:
There is a pattern which means that the red counter will move every third go, so that the red counter travels around the diagonal of the array.
In the figure below the path of the red counter from the last position, to home is represented.
Image
Overall, from this position, the red counter moves n - 2 squares down and n - 1 squares across. So we have:
n - 1 + n - 2 =2n - 3
Each time the red counter moves, two blue counters have to be moved to fill the empty space and create a new one that the red counter can move into. So, we obtain:
3(2n- 3).
Now, adding all the results to calculate the total number of moves:
(2n -3) + 1 + 3(2n -3) = 2n -3 + 1 + 6n -9 = 8n -11
Which matches the prediction.
Andrei also noted that the number of moves is always odd because 8n is always even and 11 is odd. For the 4x4 array, the red counter makes its moves on moves 6, 9, 12, 15, 18 and 21.
For the rectangular case, a similar strategy can be used.
Suppose the rectangle has $m$ rows and $n$ columns, with $m> n$.
First of all, we need $m + n - 3$ moves to get the space to next to the red counter. Then, we need use one move to put the red counter in this space.
We can then move $(n-1)$ squares down and $(n-1)$ across, using three moves per squareas before.
Now we must move down the last $(m-n-1)$ squares. This takes 5 moves for each square, as we do not alternate between horizontal and vertical moves. Adding all this up, the total number of moves needed is $$n + m - 3 + 1 + 2 \times 3(n-1) + 5(n-m-1) = 2n + 6m - 13$$