2 rings
The red ring is inside the blue ring in this picture. Can you rearrange the rings in different ways? Perhaps you can overlap them or put one outside another?
Problem
Two very special circles are on the floor:
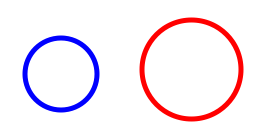
Very special because they can get bigger or smaller - as you like.
So you might like them to be like this:
Maybe you like things small - so you would have:
I'd like the blue one to grow:
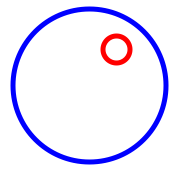
Whoa! That looks different.
The Red is inside the Blue.
So the Red and the Blue can grow - just as you like.
We've seen the Red INSIDE the Blue.
Can we change things so that we might use other words like:
Have a go. Send us some pictures of what you do - we'd love to see them.
If you enjoyed this problem, you might like to try 3 Rings .
Getting Started
How about using different sizes of hoops on the floor? I once used bracelets and rings!
How will you keep a record of what you have done? It might be useful to have some things to draw round.
Student Solutions
Alice from the Perse Senior School for Girls said:
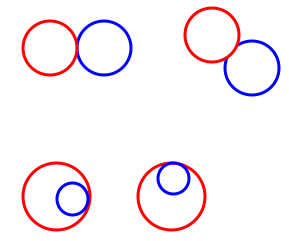
I've done 4 combinations with red and blue separate, red touching the blue, red overlapping the blue and red inside the blue.
Here are the images which Alice sent:
Image
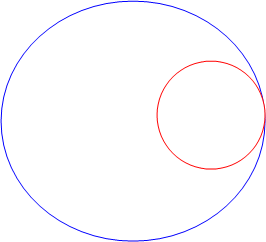
red touching blue | Image
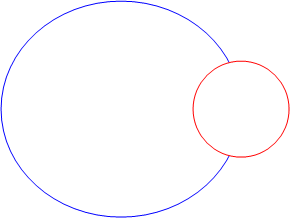
red overlapping blue |
Image
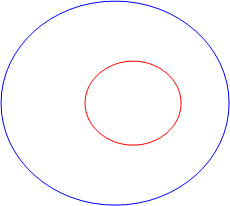
red inside blue |
Alyssa from Mason Middle School suggested:
You're right, Alyssa, you could. This would be quite difficult to draw, though, which is probably why you didn't send us an image! We would like to receive more ideas about how you could arrange two circles if you come up with some. Let us know!
Benjamin from Paradykes Primary School in Scotland sent in the following
To make the two rings touch grow one slightly bigger than the other and put the smaller one inside and touching the other ring. To make the two rings overlap then make them both same size crossing each other. For the last challenge, putting one ring outside the other you just simply make one tiny and one huge and put the tiny one inside the middle of the big one.
Thank you everyone for your contributions, you may find something similar in our Open Spaces pathway, which is part of our sister site Wild Maths.
Teachers' Resources
2 Rings
Two very special circles are on the floor:
Very special because they can get bigger or smaller - as you like.
So you might like them to be like this:
Maybe you like things small - so you would have:
I'd like the blue one to grow:
Whoa! That looks different.
The Red is inside the Blue.
So the Red and the Blue can grow - just as you like.
We've seen the Red INSIDE the Blue.
Can we change things so that we might use other words like:
Have a go. Send us some pictures of what you do - we'd love to see them.
If you enjoyed this problem, you might like to try 3 Rings .
Why do this problem?
Possible approach
Key questions
Possible extension