Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Pick's Theorem



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Abheer, Anirved, Aslesha, Asma, Dia, Eshaan, Harshad, Harshika, Jaydeep, Nishika, and Siddhanth from Ganit Kreeda in India exaplined how to work out the areas of the shapes drawn on the dotty grids. Here is their work:

Jason from Stowe School in the UK, Lexie and Fiona and Diana from Dulwich College Beijing in China and the students from Ganit Kreeda used example shapes to build up, check and refine a formula for the area.
Lexie and Fiona described their process, including the shapes they drew. Click on the image to open a larger version:
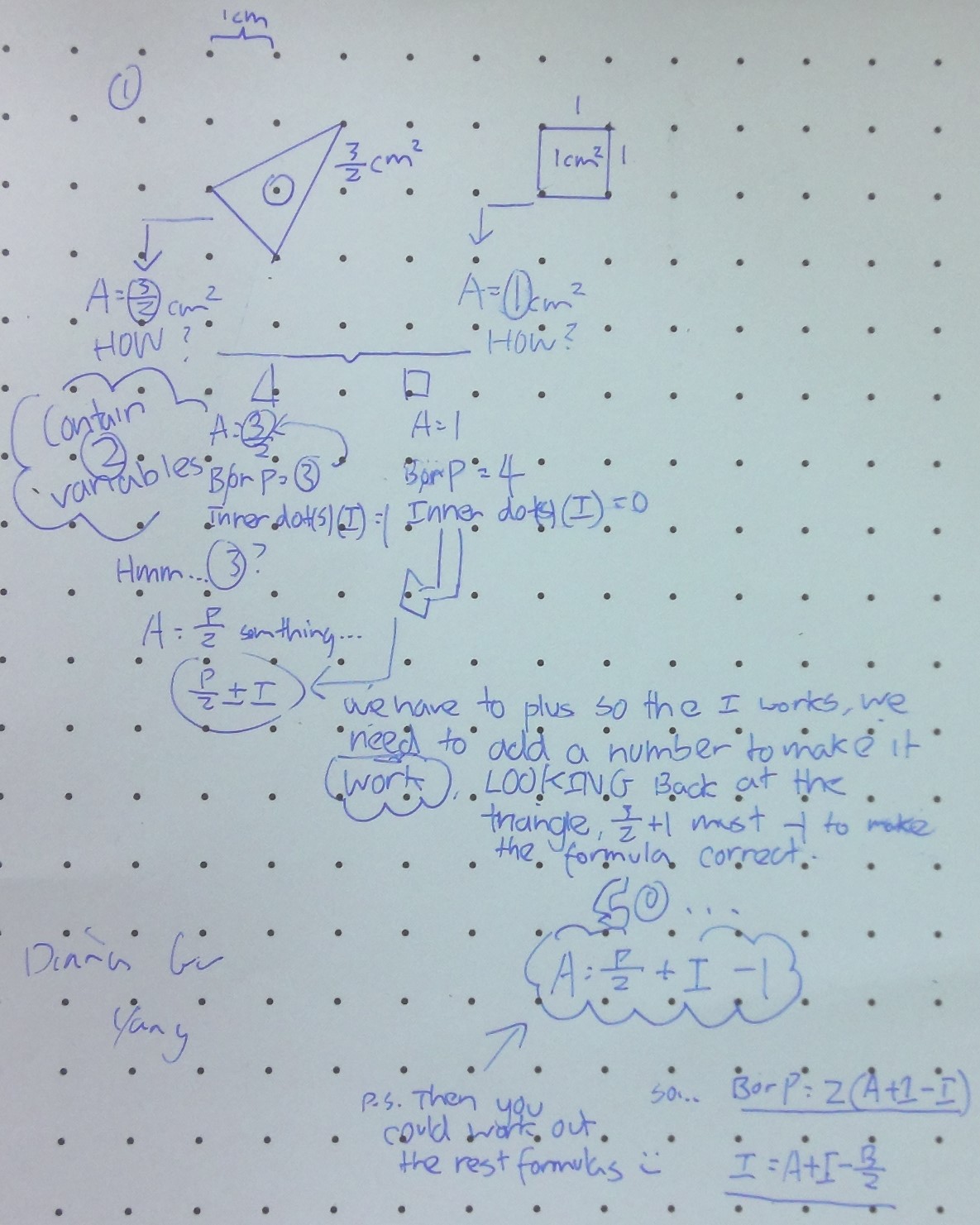
 I thought that if the area ($a$), $p$ and $i$ have a common relationship, then I should write an equation with the three variables in them. The equation I made was $a=p.i,$ but I needed to add
different mathematical symbols and also numbers. After Lexie and I drew many different shapes (triangles, quadrilaterals, pentagons, hexagons and heptagons), we started to jot notes and thoughts down.
I thought that if the area ($a$), $p$ and $i$ have a common relationship, then I should write an equation with the three variables in them. The equation I made was $a=p.i,$ but I needed to add
different mathematical symbols and also numbers. After Lexie and I drew many different shapes (triangles, quadrilaterals, pentagons, hexagons and heptagons), we started to jot notes and thoughts down.
Eventually, our equation was $a=(p\div 2)+i-1.$
For example, a pentagon on a piece of dotted paper has this piece of information:
$p: 8$
$i: 5$
$a=?$
By knowing what $p$ and $i$ are equal to, we can use this to find out the area of this shape. First, substitute the information above into the equation Lexie and I found earlier, $a=(8\div2)+5-1.$ Then, solve it. The answer should be: $a=8.$
Diana and Jason thought about separating the effects of changing $p$ and $i.$ This is Diana's work:
The students from Ganit Kreeda drew lots of shapes and used a table to help them spot patterns and find a formula:

Shaunak from Ganit Mantahn in India made a video which shows the formula in action for a large shape. Click here to see Shaunak's video.
James from Norwich School in the UK, Yuning and Harris from Stowe School in the UK and Ci Hui from Queensland Academy of Science Mathematics and Technology in Australia worked on the problem in smaller chunks. They began by considering shapes with no internal points, one internal point, two internal points and so on. This is Harris's work:
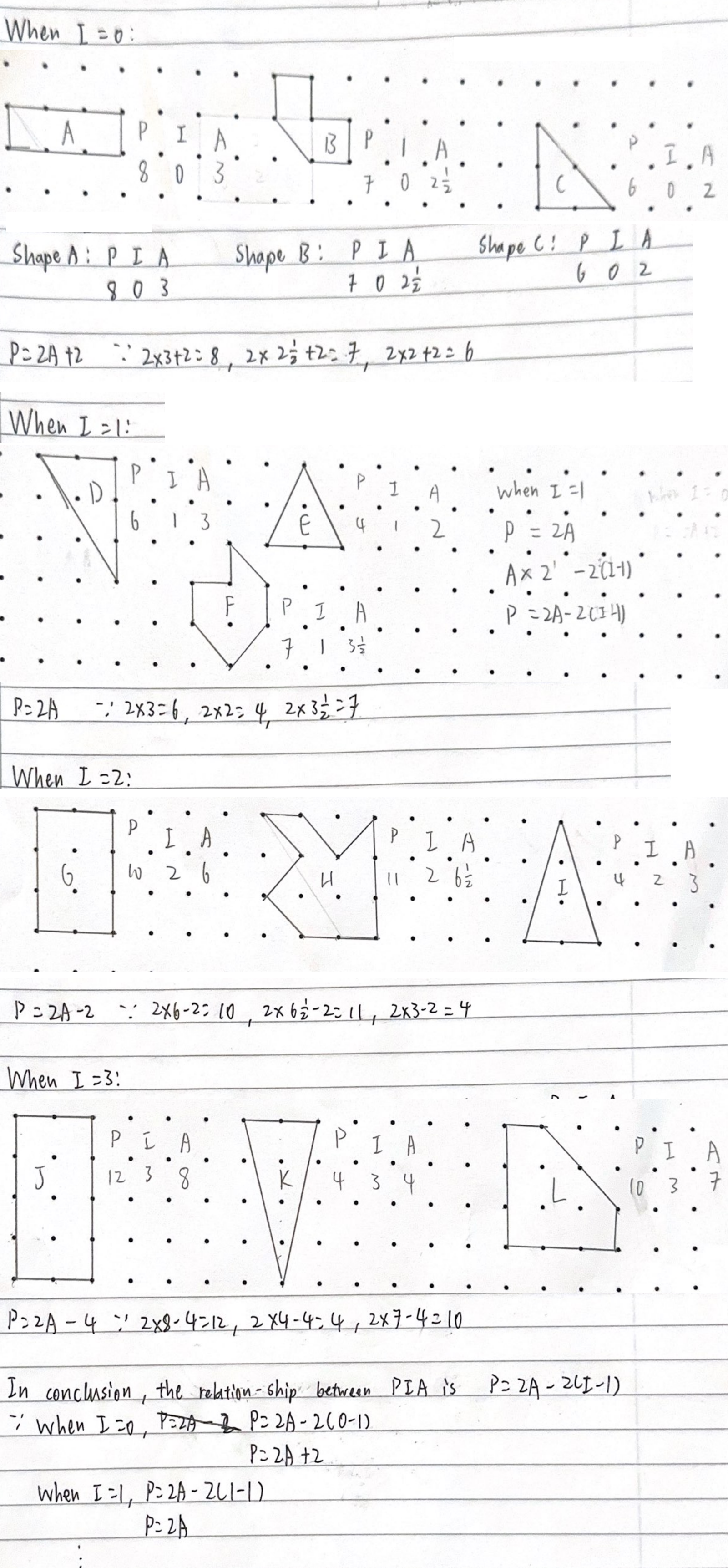
Ci Hui, Yuning and James all found the same relationship, but wrote the formula so that $A$ was the subject. Ci Hui included a table to record and interpret the results. Below is Ci Hui's table and conculsion (click on the image to open a larger version), and click here to see Ci Hui's diagrams.
Aidan, Will, Bryan, Tony and Daniel from Dulwich College Beijing in China found the same formula using simultaneous equations:
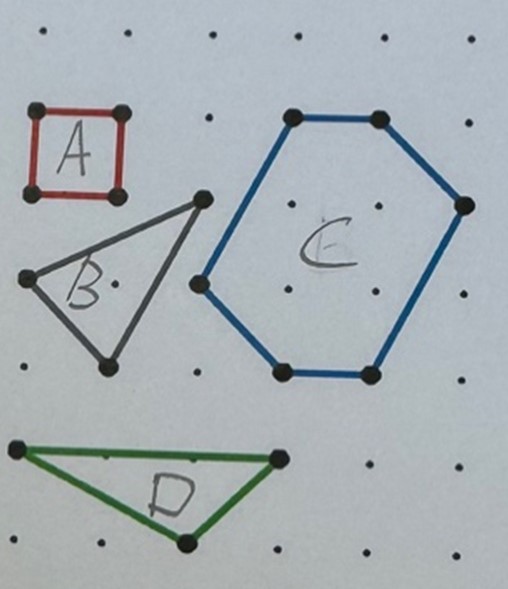
Here is a list on the P and I and their area to find relations between them. (We are saying that the between each dot is 1.):
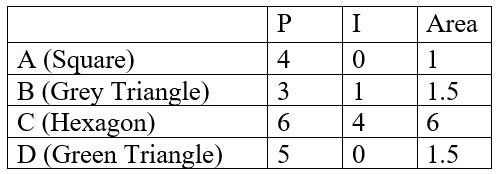
From the data above, we had assumed that the Pick’s Theorem is an equation, in form of “$A=aP+bI+c$”, there, we got the following equations:
Equation 1: $4a+c=1$ (shape A)
Equation 2: $5a+c=1.5$ (shape D)
Subtracting equation 1 from 2, we get:
$a = 0.5$
Substituting the data from shape D into equation 2, we got $a=0.5, c=-1$
Now with $a$ and $c,$ we can easily work out that $b=1.$
With this we can work out that the equation
Which is $A=ap+bi+c=0.5p+i-1=\frac p 2 +i-1$
Having found the formula, Aidan, Will, Bryan, Tony, and Daniel decided to prove that it will always work. Their proof uses a related theorem, called Euler's Theorem, which is closely related to Pick's Theorem. Here is their proof (click on the image to open a larger version):
Now, after we had done trying to work out the theorem, we should start to [prove] the equation:
The students from Ganit Kreeda thought about shapes with the same area:

These ideas come directly from the formula. If you wanted to prove the formula, you could work backwards from these ideas. Look at these examples of removing one interior point and adding two perimeter points. Can you explain why the area is always the same?

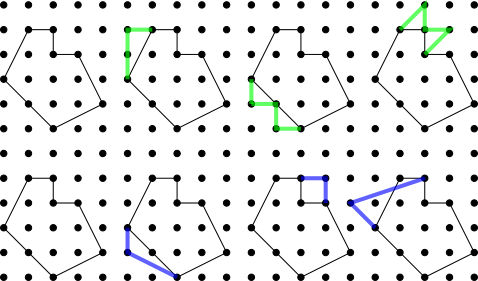
The students from Ganit Kreeda also explored how you can increase the area by 1 unit:

These ideas come directly from the formula. If you wanted to prove the formula, you could work backwards from these ideas. Look at these examples of adding two perimeter points or one interior point. Does the area always increase by 1?