Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Pair Products



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Barbora from Parklane International School in the Czech Republic wrote about the patterns in the numbers:
I have noticed that the product of the middle pair is always 2 larger than the product of the outer pair. I have also noticed that the sum of the 1st and 4th number is equal to the sum of the 2nd and 3rd number. Furthermore, the 3rd number is always 2 larger than the 1st number and the 4th number is always 2 larger than the 2nd number. I think that these things will always happen because the numbers are arranged in the same order each time, so there isn't any variation in the pattern other than the integers used. The pattern is always: $n, n + 1, n + 2, n + 3$
Lyle, Caden and Michael from Cockburn Laurence Calvert Academy used Barbora's idea to explain what happens to the products. This is Lyle's work:
| 4 consecutive numbers | Multiply first and last numbers | Multiply middle pair | Notes |
| 1, 2, 3, 4 | 1 $\times$ 4 = 4 | 2 $\times$ 3 = 6 | difference of 2 |
| 2, 3, 4, 5 | 2 $\times$ 5 = 10 | 3 $\times$ 4 = 12 | difference of 2 |
| 10, 11, 12, 13 | 10 $\times$ 13 = 130 | 11 $\times$ 12 = 132 | difference of 2 |
| 1000, 1001, 1002, 1003 | 1000 $\times$ 1003 = 1003000 | 1001 $\times$ 1002 = 1003002 | difference of 2 |
Solution
$\begin{align}&n\hspace{3mm}\times \hspace{3mm}n+3&\hspace{15mm}&n+1\hspace{3mm}\times \hspace{3mm}n+2\\
&n^2+3n& &n^2+3n+2\end{align}$
Difference of 2
Ben from Comberton Village College in the UK, Andrew from Kellett in Hong Kong and Ella from Parklane International School also used the same algebra as Lyle. Andrew repeated the process for sets of 6 and 10 consecutive numbers (click on the image to open a larger version):
Matouš and Matyáš from Parklane International School in the Czech Republic wondered what the difference would be for other numbers of consecutive numbers, like 154. Here is their work:
For any number of consecutive numbers:
$x$ = total number of consecutive numbers
$y$ = the difference between the two products (1st $\times$ last and 2nd $\times$ penultimate)
Eg. If we use all the consecutive numbers between and including 1 and 154.
$x$ = 154
1 $\times$ 154 = 154 (1st $\times$ last)
2 $\times$ 153 = 306 (2nd $\times$ penultimate)
$y$ = 306 $−$ 154 = 152
Have they made any assumptions?
Freya from Comberton Village College applied the same method to numbers that are not consecutive, but go up in threes:
The sequence I chose goes up in threes. For my example, I used 2,5,8,11.
Outer pair: 2$\times$11=22
Inner pair: 5$\times$8=40
40$-$22=18
To explain this, I used algebra.
$n(n+9)=n^2+9n$
$(n+3)(n+6)=n^2+9n+18$
$(n^2+9n+18)-(n^2+9n)=18$
Imaan from Walton High School in England investigated several different numbers of numbers and distances between the numbers. Here is Imaan's work (click on the image to open a larger version):
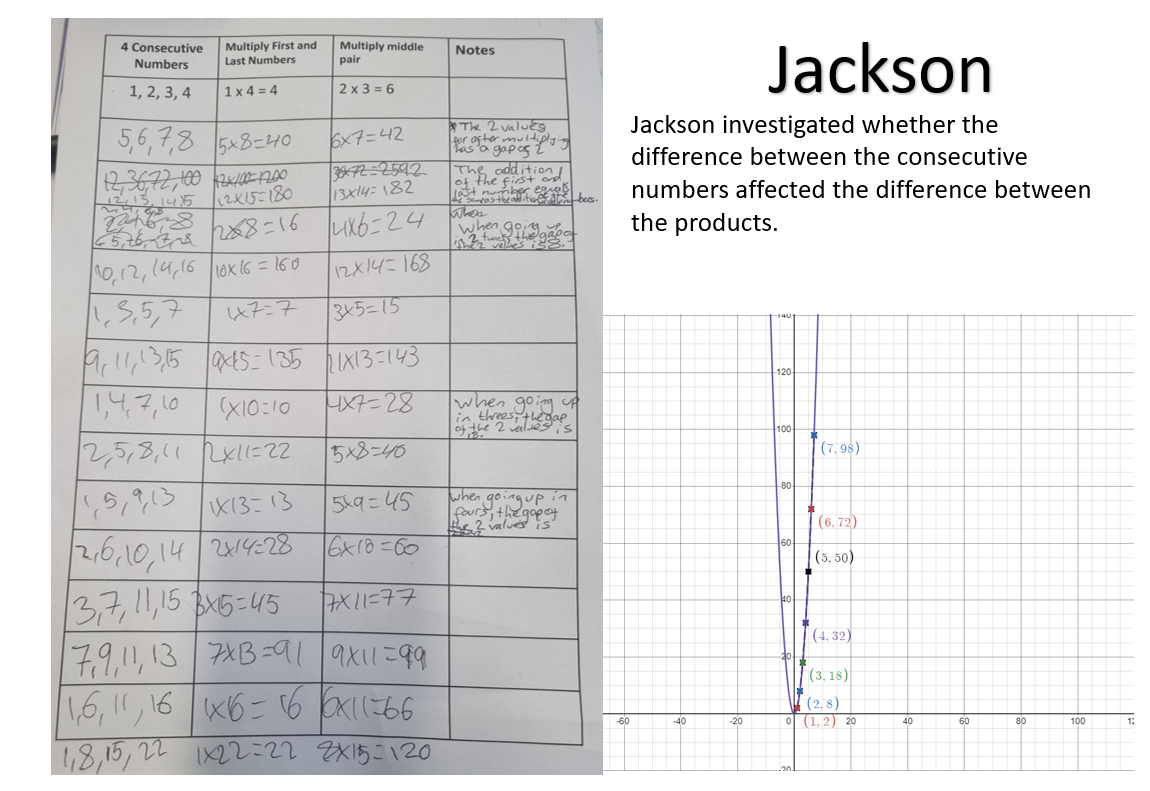
Sophia and Bianca from Kellet and Jackson from Cockburn Laurence Calvert Academy tried out different differences between the numbers in a systematic way. This is Jackson's work, which includes a graph (click on the image to open a larger version):
Alain, Teodor and Fabian from Parklane International School and Andrew Chambers's students at British International School Phuket in Thailand both wrote up lots of ideas, rules and proofs - including things which could be used to explain the shape of Jackson's graph. The British International School Phuket students really enjoyed this task and spent 2 full lessons working on it. They worked out the difference between the products of the first and last and the the middle two numbers, rather than the first and last and the second and penultimate numbers:
Click here to see the British International School Phuket students' work, and click here to see Alain, Teodor and Fabian's work. Both also include explorations of when the numbers are all even, or all odd.
Venya from the British International School Phuket considered a very general case, where there are $n$ numbers that go up in steps of $q$:
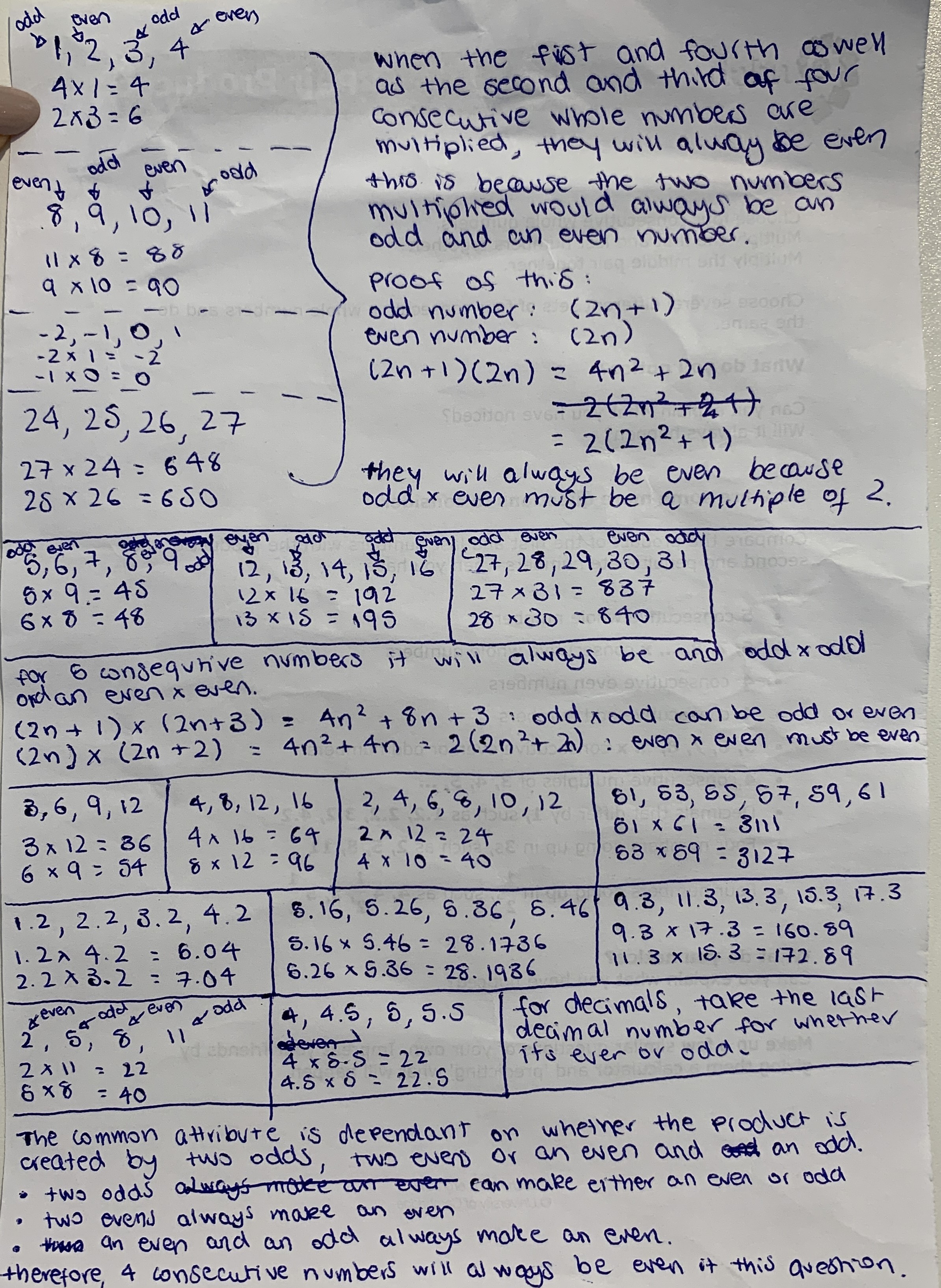
Zara from St James Senior Girls School carried out a slightly different investigation into whether the products were even or odd (click on the image to open a larger version).