Proving Half-angle Formulae
Problem
Take a look at the identities below.
$$ \cos^2 \frac{\theta}{2} \equiv \frac{1}{2}(1+\cos \theta) \quad \quad \quad \sin^2 \frac{\theta}{2} \equiv \frac{1}{2}(1-\cos \theta)$$
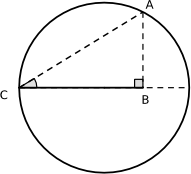
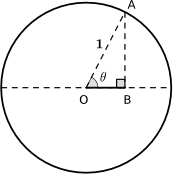
You may well know enough trigonometric identities to be able to prove these results algebraically, but you could also prove them using geometry. We have provided some diagrams that may help you to prove the result for $\cos^2 \frac{\theta}{2}$. Can you link the diagrams together to form a proof?
You may find it helpful to group the diagrams together in different ways or look for links between pairs of diagrams. You don't need to use all the diagrams in your proof and you may prefer to add some of your own diagrams. The diagrams are available as a print out. There is an extra card in case you'd like to include another diagram in your proof.
cards.pdf 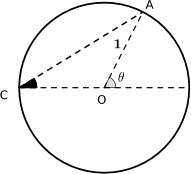
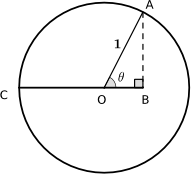
Can you prove the result for $\sin^2 \frac{\theta}{2}$ in a similar way?
Underground Mathematics is hosted by Cambridge Mathematics. The project was originally funded by a grant from the UK Department for Education to provide free web-based resources that support the teaching and learning of post-16 mathematics.
Visit the site at undergroundmathematics.org to find more resources, which also offer suggestions, solutions and teacher notes to help with their use in the classroom.
Getting Started
Can you relate the diagrams to either the left-hand side of the identity or to the right-hand side?
Is there a diagram that shows a length that corresponds to $1+\cos \theta$?
Student Solutions
Well done to Jessica from Tiffin Girls' School and Minhaj from St Ivo School who both found proofs of the two identities using these diagrams.
Jessica's idea, for both identities, was to use the two right angled triangles $\triangle AOB$ and $\triangle ACB$ in the diagram below.
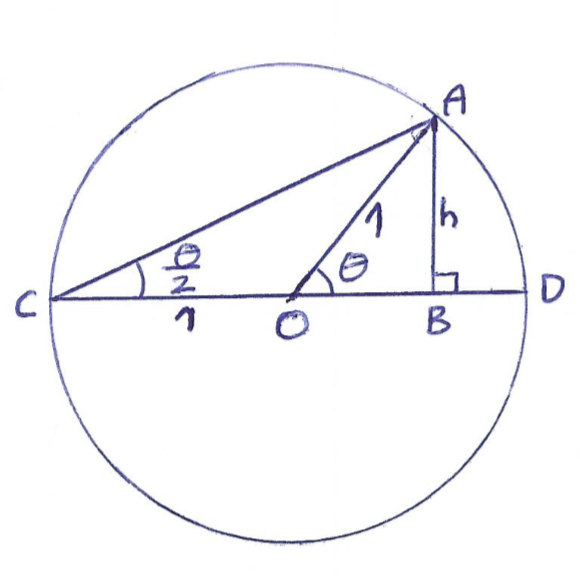
To prove $\cos^2{\frac{\theta}{2}} \equiv \frac{1}{2}(1+\cos{\theta})$
In $\triangle AOB$:
$OB=\sqrt{1-h^2}$ (by using Pythagoras' Theorem)
$\cos{\theta}=\frac{OB}{OA} =\sqrt{1-h^2}$
$h^2=1-\cos^2{\theta}$
In $\triangle ACB$:
$BC=BO+OC=1+\sqrt{1-h^2}$
$AC^2=AB^2+BC^2=h^2+(1+\sqrt{1-h^2})^2$
$\cos^2{\frac{\theta}{2}}=\frac{BC^2}{AC^2}=\frac{(1+\sqrt{1-h^2})^2}{(1+\sqrt{1-h^2})^2+h^2}$
Since we know $\cos{\theta}=\sqrt{1-h^2}$ and $h^2=1-\cos^2{\theta}$ we can get this in terms of $\cos{\theta}$:
$\cos^2{\frac{\theta}{2}}=\frac{(1+\cos{\theta})^2}{(1+\cos{\theta})^2+1-\cos^2{\theta}}=\frac{(1+\cos{\theta})^2}{2+2\cos{\theta}}=\frac{1}{2}(1+\cos{\theta})$
To prove $\sin^2{\frac{\theta}{2}} \equiv \frac{1}{2}(1-\cos{\theta})$:
In $\triangle AOB$:
$\sin{\theta}=\frac{AB}{AO}=\frac{h}{1}=h$
In $\triangle ACB$:
$\sin^2{\frac{\theta}{2}}=\frac{h^2}{(1+\sqrt{1-h^2})^2+h^2}$
As in the previous proof we can use $\cos{\theta}=\sqrt{1-h^2}$ and $h^2=1-\cos^2{\theta}$ to get:
$\sin^2{\frac{\theta}{2}}=\frac{1-\cos^2{\theta}}{(1+\cos{\theta})^2+1-\cos^2{\theta}}=\frac{(1+\cos{\theta})(1-\cos{\theta})}{2(1+\cos{\theta})}=\frac{1}{2}(1-\cos{\theta})$
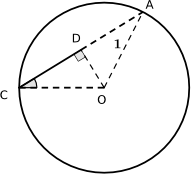
Minhaj found an alternative way to prove these identies using different diagrams. Here is his proof of $\cos^2{\frac{\theta}{2}} \equiv \frac{1}{2}(1+\cos{\theta})$.
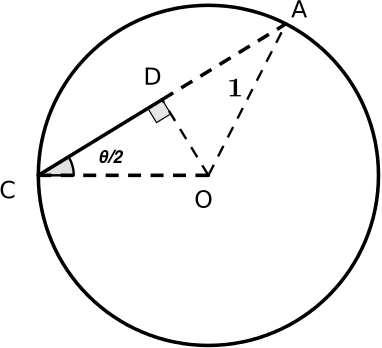
Note: In triangle AOC, lines CD and DA are equal (circle theorem: OD passes through the centre of the circle and is the perpendicular bisector of the chord CA, therefore since it bisects CA, CD=DA)
1. $\cos{\frac{\theta}{2}} = \frac{CD}{1}=CD$. Since $CD=DA$, $DA=\cos{\frac{\theta}{2}}$ too.
2. So $CA = CD + DA = 2 \cos{\frac{\theta}{2}}$
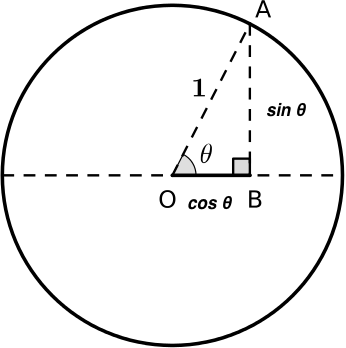
3. Have that $CB = \cos{\theta}+1$ and $AB = \sin{\theta}$
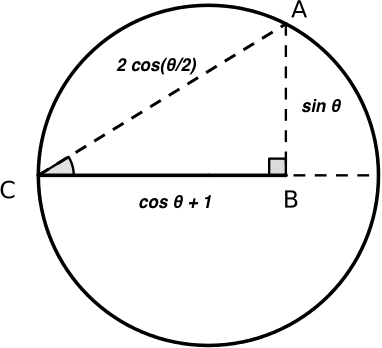
4. From Pythagoras' theorem have that $CB^2 + AB^2 = CA^2$,
so $(\cos{\theta}+1)^2 + \sin^2{\theta} = 4 \cos^2{\frac{\theta}{2}}$
5. Substituting $\sin^2{\theta} = 1-\cos^2{\theta}$ and rearranging gives:
$(\cos{\theta}+1)^2+(1-\cos^2{\theta}) = 4\cos^2{\frac{\theta}{2}}$
$cos^2{\theta}+2\cos{\theta}+1+1-\cos^2{\theta}=4\cos^2{\frac{\theta}{2}}$
$2 \cos{\theta}+2 = 4\cos^2{\frac{\theta}{2}}$
$\cos^2{\frac{\theta}{2}}=\frac{1}{2}(\cos{\theta}+1)$
Yet another way to complete this proof after point 3 without using pythagoras could be to look at the expression for $\cos{\frac{\theta}{2}}$ in the triangle $ACB$.

