Maxagon
What's the greatest number of sides a polygon on a dotty grid could have?
Problem
For this problem you may wish to download and print some dotty paper.
Alternatively, you could explore the problem using this interactivity.

Draw some polygons by joining the dots on a $3$ by $3$ grid.
What is the greatest number of sides that your polygon could have?
What about on a $3$ by $4$ grid, or a $3$ by $5$ grid?
What about on a $3$ by $n$ grid?
Can you explain the pattern by which the 'number of sides' increases?

Explore some polygons on grids that are $4$ dots high.
What is the maximum number of sides a polygon could have on a $4$ by $n$ grid?
Can you explain how you know?

What is the maximum number of sides a polygon could have on a $6$ by $6$ grid?
And on a $6$ by $n$ grid?
With thanks to Don Steward, whose ideas formed the basis of this problem.
Getting Started
Will the patterns be different depending on whether $n$ is even or odd?
Student Solutions
Students in the mathematics extension group from Lyneham Primary School sent us this solution. Thank you and well done to them.
The students started with $3 \times 3$ grids and found that the maxagon had $7$ sides.
When they used $3 \times 4$ grids, they found that the maxagon had $10$ sides.
Jack and Huon suggested a "rule" which would say how many sides the maxagon had, and Brendan used the rule to predict that a maxagon on a $3 \times 5$ grid would have $13$ sides. At the same time, Cate, Ruby and Kristina, who were working on $3 \times 5$ grids, found a maxagon with $13$ sides.
Fergus and Cate found a rule for these maxagons: for a $3 \times n$ grid, if you make as many sides as possible, then there will be $3 \times n - 2$ sides.
The group were also able to explain methods for making these maxagons on $3 \times n$ grids:
Khubaib and Brendan explained how they could add units onto their maxagon to make it larger:
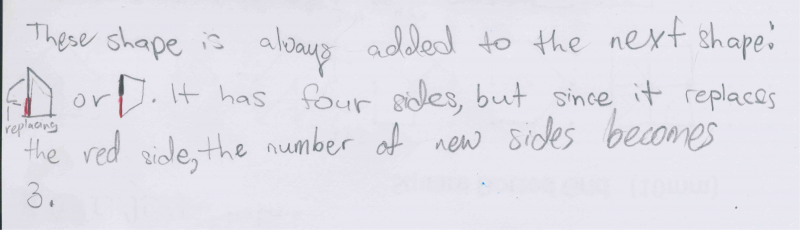
Cate was then able to use this process to show how to make some maxagons:

Alex described this process as being like a train, where you have an engine at the front (in Cate's diagram this is the part in blue), and then a number of carriages, which are the sections in the two different pink sections.
Khubaib and Brendan were then able to extend this to make a long maxagon:

Alexia from Wycombe High School looked at the $4 \times n$ case and sent us this excellent solution. Well done!
I looked at the maxagons with a grid that is 4 dots high and found this pattern:

Seb and Max from Landscore Primary School had this to show us about the $5 \times n$ case. Good work!
The number of sides is always 2 less than the number of dots. For example, if it has 25 dots ($5 \times 5$), the maximum number of sides will be 23. $5 \times 5$:

This also applies to non square numbers such as 30 dots ($5 \times 6$) would have 28 sides. We tried this with many drawings and calculations spending over 1 hour testing this theory and others.
Jessica sent us the following solutions for the $6 \times n$ case.
The maximum number of sides of a polygon constructed on the grid will be reached when each dot is the end point of two sides (if it were the end point of more sides, then we would not have a polygon). On a $6\times n$ grid, we have $6n$ dots. Since each dot connects to two sides, this would give us $2\times6\times n$ sides, but we have counted each side twice. So we then need to halve that to get $\frac{2\times 6n}{2}=6n$ as the maximum number of sides.
Here are two $36$-sided polygons for the $6\times6$ grid, which is the maximum we can achieve.


Using one of these models, we can get a pattern for a $6\times n$ grid, where $n$ is even.

We now need to create a pattern for the odd values of $n$. We will start with creating one for $n=7$ and afterwards we generalize it.

So the maximum number of sides for a $6\times n$ grid seems to be $6n$. This is indeed the case, since we formed the polygon on a $6\times n$ grid from the one on a $6\times (n-2)$ grid (for every $n>7$) by adding $12$ sides, namely the red sides from the pictures below.


