Pieces of eight
Two of the triangles in the diagram are shaded black. What is the probability the resulting figure has at least one line of symmetry?
Age
11 to 14
Challenge level
Problem
A square is divided into eight congruent triangles, as shown.
Image
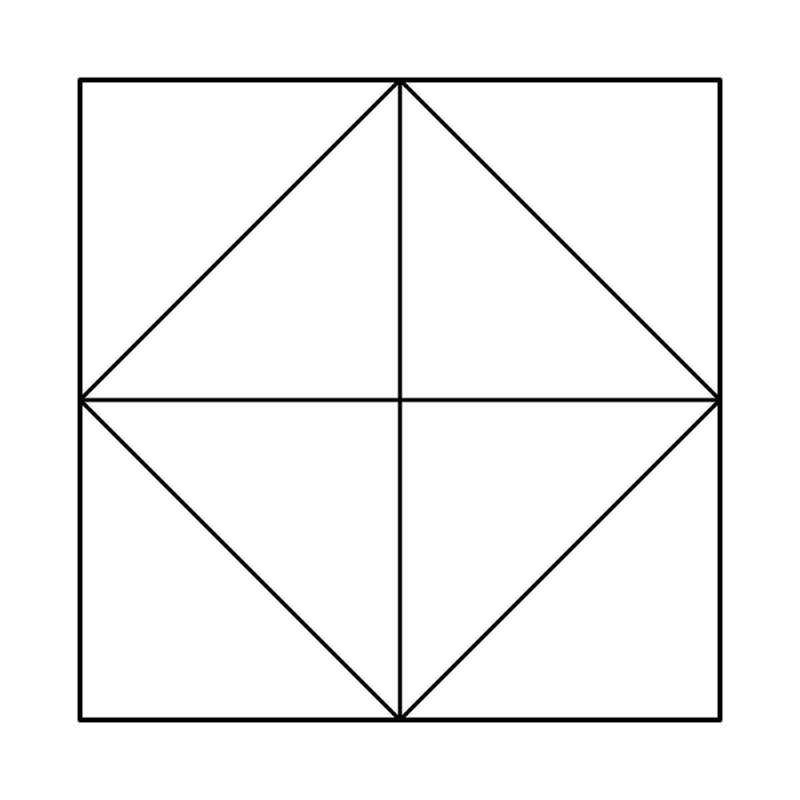
Two of these triangles are selected at random and shaded black.
What is the probability that the resulting figure has at least one line of symmetry?
If you liked this problem, here is an NRICH task that challenges you to use similar mathematical ideas.
Student Solutions
If the first triangle selected to be shaded is a corner triangle, then the final figure will have at least one line of symmetry provided that the second triangle selected is one of five triangles. For example, if A is chosen first then there will be at least one line of symmetry in the final figure if the second triangle selected is B, D, E, G or H.
The same applies if an inner triangle is selected first: for example, if B is chosen first then there will be at least one line of symmetry in the final figure if the second triangle selected is A, C, F, G or H.
Image
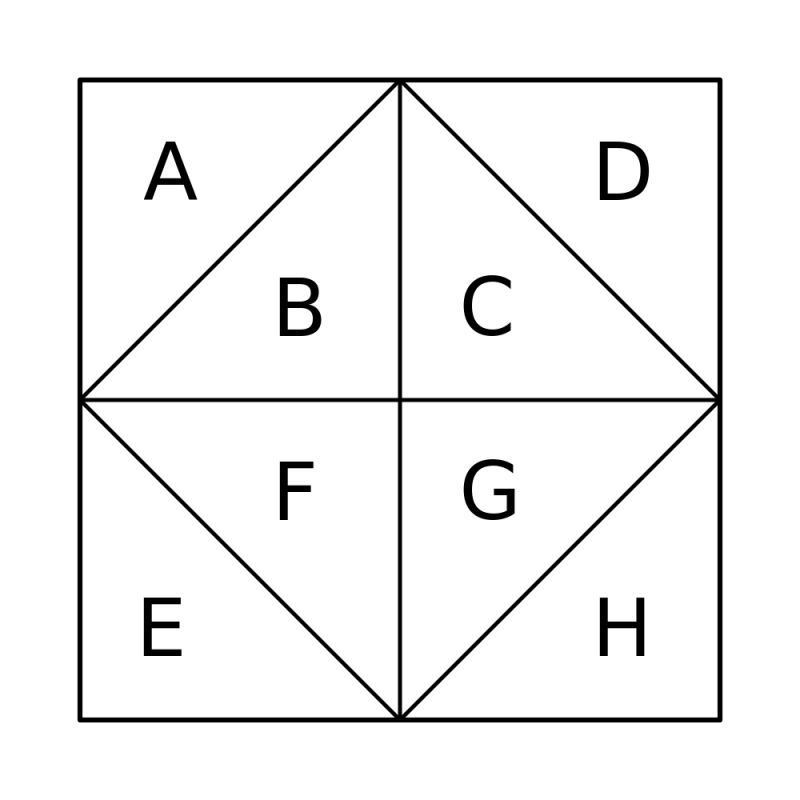
So, the probability that the final figure has at least one line of symmetry is $\frac{5}{7}$.