L-triominoes
L triominoes can fit together to make larger versions of themselves. Is every size possible to make in this way?
Problem
A triomino is a shape made from three squares. Here is an L-triomino:
Image
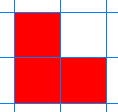
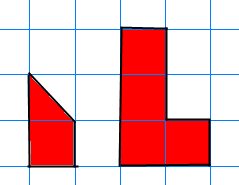
Here is a size 2 L-triomino:
Image

It can be tiled with four size 1 L-triominoes:
Image

Can you work out how to use the tiling of a size 2 L-triomino to help you to tile a size 4 L-triomino? Click here for a hint.
Devise a convincing argument that you will be able to tile a size 8, 16, 32... $2^n$ L-triomino using size 1 L-triominoes.
How many size 1 L-triominoes would you need to tile a size 8... 16... 32... $2^n$ L-triomino?
What about odd sized L-triominoes? The diagram below shows the region which needs to be tiled to turn a size 1 L-triomino into a size 3 L-triomino.
Image
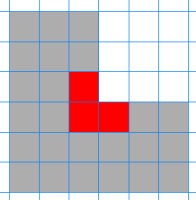
Image
In the same way, can you find a way of adding to your size 3 tiling to tile a size 5? Then a size 7, 9, 11...? Click here for a hint.
Devise a convincing argument that you will be able to tile any odd sized L-triomino using size 1 L-triominoes.
Combine your ideas to produce a convincing argument that ANY size of L-triomino can be tiled.
Here is an interactive you could use to try out your ideas.
Getting Started
Look at the picture below showing different odd sizes of
triomino.
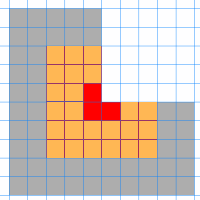
Can you see a way to build round the red triomino to make the orange one?
To build round the orange one to make the grey one?
Can you continue to make a size $7$ triomino? And then a size $9$?
Image

Can you see a way to build round the red triomino to make the orange one?
To build round the orange one to make the grey one?
Can you continue to make a size $7$ triomino? And then a size $9$?
Student Solutions
Neerajan and Eilidh both noticed that the number of L-triominoes needed to tile a size $n$ L-triominoes was equal to $n^2$.
Philip from Wilson's School explained his thinking:
To tile a size 4 triomino you would simply put 4 size 2 triominoes together the same way you put four size 1 triominoes together to make a size 2.
Therefore you would put 4 size 4 triominoes together in the same way to form a size 8 triomino. Then 4 size 8 triominoes to make a size 16, and so on.
The triominoes could therefore tile size 8, 16, 32... $2^n$. These can therefore be made up of size 1 triominoes.
As it takes $4^1$ size 1 triominoes to tile a size 2 triomino, and $4^2$ size 1 triominoes to tile a size 4 triomino, it would therefore take $4^3=64$ size-1 triominoes to tile a size 8 triomino.
It would then take $4^4=256$ size 1 triominoes to tile a size 16 triomino and $4^5=1024$ size 1 triominoes to tile a size 32 triomino.
Finally, it would take $4^x$ triominoes to tile a size $2^x$ triomino.
To tile the size 3 triomino you simply use the 2x3 rectangular blocks at the top and on the right and then the rest you use a size 2 triomino and the size 1 in the middle.
To tile a size 5 triomino you simply add another size 2 triomino in the bottom left and for the rest you can use the 2x3 rectangular boxes.
Issac from Hampton School also managed to explain how to construct trionimoes of size $2^n$, and of size $3$ - well done Isaac!
Rajeev from Habedashers' Aske's Boys' School managed to find a way to colour a size-7 trionimo:
Image

Thank you to everybody for thinking so hard about this problem.
The submitters above have managed to show that we can tile any L-trionimo of size $2^n$ by splitting it into four L-trionimoes of size $2^{n-1}$, all the way back to size-1 trionimoes. Now, let's think about how we can show that we can tile any L-trionimo of odd size:
Obviously, we can tile a size-1 trionimo with itself. Phillip, Isaac and Rajeev have shown above that it's possible to to tile trionimos of sizes three, five, and seven.
Suppose we have a trionimo of size $n$, where $n$ is an odd number, and we know that we can use L-trionimos to tile a trionimo of size $n-2$ (i.e. the next odd number down). Can we use this fact to help us tile our trionimo?
Let's try splitting our trionimo into a size $(n-2)$ trionimo and a surrounding L-shape:
Image
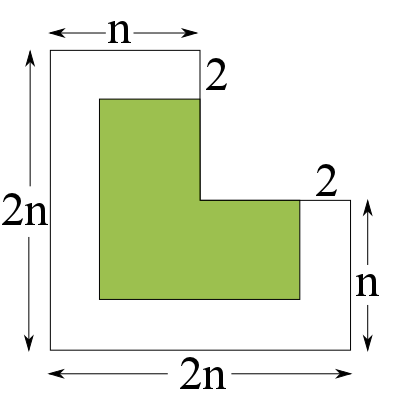
We are assuming we can tile the green area (the size $(n-2)$ trionimo). If we can find a way to tile the surrounding white area, then we can tile the whole shape and we are done.
Can we do this?
Yes! In fact, it is always possible (for any odd number $n$) to tile this area using only our two building blocks from before: the size-$2$ trionimo, and the $2 \times 3$ rectangle obtained by joining two trionimos together.
Let's try putting a size-$2$ trionimo in the bottom-left-hand corner of our shape:
Image
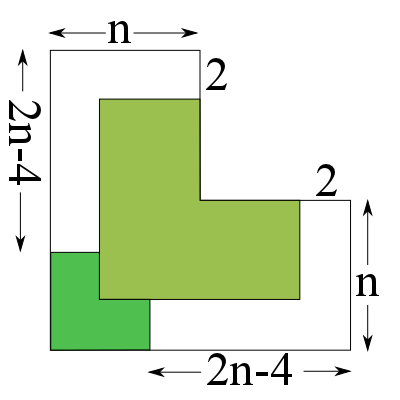
This leaves us with two white L-shapes to tile. We can see though, by the symmetry of the triomino, that these L-shapes are mirror images of each other, and so if we can find a way to tile one of them, we can easily use this to tile the other shape, and we are done. Let's focus on the bottom-right hand area:
Image
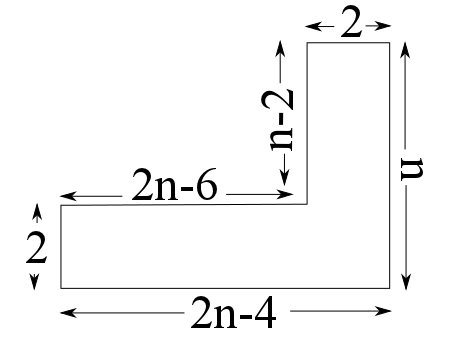
How can we tile this area using our building blocks? This time, the answer depends on $n$.
Every number $n$ is either a multiple of $3$, has remainder $1$ when divided by $3$, or has remainder $2$ when divided by $3$.
If $n$ is a multiple of $3$, the right-hand side of this shape (the vertical $2 \times n$ rectangle) can be covered completely with a line of $2 \times 3$ rectangles. This leaves a $(2n-6) \times 2$ rectangle untiled. However, if $n$ is a multiple of three, then so is $2n$, and as $6$ is a multiple of $3$ then so is $2n-6$. This means we can cover this remaining rectangle with another line of $2 \times 3$ rectangles, and we have successfully tiled the whole shape.
If $n$ has remainder $1$ when divided by $3$, we can fill in the bottom-right corner with a size-$2$ trionimo. This leaves us with two separate rectangles to fill in: a vertical one of size $2 \times (n-4)$, and a horizontal one of size $(2n-8) \times 2$.
As $n$ has remainder $1$ when divided by $3$, $n-1$ must be a multiple of $3$. Subtracting $3$ from this, we can see that $n-4$ is also a multiple of $3$ and so we can fill in our $2 \times (n-4)$ rectangle with a column of $2 \times 3$ rectangles.
Doubling a multiple of $3$ gives another multiple of $3$, so $2 \times (n-1) = 2n-2$ must also be a multiple of $3$. Subtracting $6$ (another multiple of $3$) from this, we can see that $2n-8$ is a multiple of $3$, so we can tile our $(2n-8) \times 2$ rectangle with a row of $3 \times 2$ rectangles, and we are done.
If $n$ has remainder $2$ when divided by $3$, $n-2$ must be a multiple of $3$. Doubling this, we can see that $2n-4$ must also be a multiple of three. This means that we can tile the bottom of this L-shape (the $(2n-4) \times 2$ rectangle) with a row of $3 \times 2$ rectangles, leaving a vertical rectangle of dimensions $2 \times (n-2)$. However, we know that $n-2$ is also a multiple of three, so we can also fill in this rectangle with a column of $2 \times 3$ rectangles, and we are done.
So, regardless of what $n$ actually is, we can find some way to tile the white shape with trionimoes.
This now means that we can tile every trionimo of odd size!
Why?
We assumed that we already know how to tile a trionimo of size $n-2$. This means we now know that if we can tile a trionimo of size $n-2$, we can also tile a trionimo of size $n$ (as long as $n$ is odd).
However, Phillip, Isaac and Rajeev have shown how to tile a trionimo of size $3$.
Using what we have shown above, this means we can tile a trionimo of size $5$.
But if we can tile a trionimo of size $5$, we can tile a trionimo of size $7$!
And if we can tile a trionimo of size $7$, we can tile a size-$9$ triomino...
Carrying on like this, we can now see that we can tile any trionimo of odd size, no matter how big it is.
Can we combine everything we've done to show that we can, in fact, tile a triomino of any size?
Let's take a triomino of size $n$. If $n$ is odd, we know that we can tile it, so let's assume that $n$ is even.
Then, in exactly the same way that we tiled a size-$2^n$ triomino with four size-$2^{n-1}$ triominoes, we can use four triominoes of size $\frac{n}{2}$ to tile our trionimo.
How does this help?
Well, if we can tile each of these four triominoes, we can certainly tile the whole shape. So we know that if we can tile a trionimo of size $\frac{n}{2}$, we can tile a trionimo of size $n$.
If $\frac{n}{2}$ is odd, we know that we can tile it, and we're done.
If $\frac{n}{2}$ is even, we can repeat the entire process: tile a $\frac{n}{2}$-size trionimo with four size-$\frac{n}{4}$ trionimoes and we can see that if we can tile a size-$\frac{n}{4}$ triomino, we can tile a size-$n$ triomino.
If $\frac{n}{4}$ is odd, then we're finished, and if it's even we repeat the process again.
No matter how many times we have to repeat this process, eventually we'll stop at an odd number.
(Can you see why this is?)
So eventually, we will be able to find an odd number $m$ such that we can tile our trionimo with size-$m$ triominoes.
As $m$ is odd, we know that we can replace each size-$m$ trionimo with a tiling of $m^2$ single triominoes, and we have found a way to tile our size-$n$ triomino with single L-triominoes.
This works for any even number $n$.
So we can tile any odd-sized triomino and any even-sized triomino. Putting this together, we can tile any triomino using size-$1$ triominoes!
Teachers' Resources
Why do this problem?
This problem begins with very simple ideas about tiling and enlargement but can lead learners to appreciate how proofs can be built up in stages, through breaking an idea down into special cases. It also introduces the intriguing mathematical notion of reptiles - shapes that can be tiled to make enlargements of themselves.Possible approach
Start by introducing the
smallest L-triomino and challenge learners to find a way to tile a
size 2, 3 and 4 L-triomino with it, on squared paper. They may work
in quite a haphazard way to start off with, and may not even find
ways of tiling them all. There is the opportunity to discuss the
number of tiles needed, and to make links with work on enlargements
and similar shapes.
Once everyone has had a
go at tiling the first few L-triominoes, and successful attempts
are collected on the board for all to see, follow up with: "I wonder whether all sizes of
L-triomino can be tiled"
Suggest the need for a
systematic approach, gradually building up knowledge of how
different sizes of L-triomino can be tiled.
Ask learners to start by
considering how the tiling of the size 2 L-triomino helps in tiling
the size 4 L-triomino. Can they develop their ideas further and
suggest how they would convince someone that all size $2^n$
L-triominoes can be tiled? Bring the class together to share their
insights.
Next, introduce the odd
numbered sizes of L-triominoes. Share these diagrams with the
class:
Image

Image
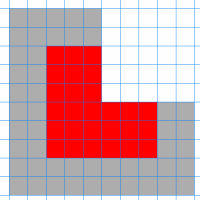
Challenge learners to
find simple ways of extending their tilings from one odd number to
the next, in a way that will lead to a convincing argument that all
odd sized L-triominoes can be tiled.
Finally, learners need to
consider how the two arguments can be combined to prove that all
L-triominoes can be tiled - this is a good opportunity to discuss
the formal steps in writing down a mathematical
argument.
Key questions
How can I use my
knowledge of tiling a size 2 L-triomino to tile a size 4?
How can I use my
knowledge of tiling a size 3 L-triomino to tile a size 5?
How can I use my
knowledge of tiling odd and $2^n$ sized L-triominoes to tile
ANY size L-triomino?
Possible extension
Investigate tilings with
these other reptiles:
Image
Come up with similar
proofs that all sizes can be tiled.
