Hamiltonian Cube
Weekly Problem 36 - 2007
Find the length along the shortest path passing through certain points on the cube.
Find the length along the shortest path passing through certain points on the cube.
Age
11 to 16
Challenge level
Problem
Visiting all the vertices
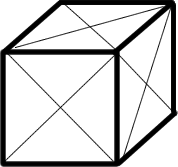
The figure shows a cube with sides of length $1$, on which all twelve face diagonals have been drawn - creating a network with $14$ vertices (the original eight corners, plus the six face centres) and $36$ edges (the original $12$ edges of the cube plus four extra edges on each face). What is the length of the shortest path along the edges of the network which passes through all $14$
vertices?
Image
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
Image
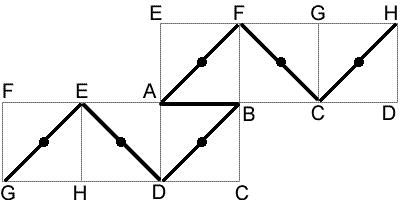
The image above shows a possible path. Each edge joining a corner to a face centre has length $\frac{1}{\sqrt{2}}$ (by Pythagoras' Theorem), while each edge which joins two adjacent corners has length $1$. So the length of the path above is $1+6\sqrt{2}$. This is the length of the shortest path to pass through all the vertices.
To prove this, note the length of the shortest path must be at least $\frac{13}{\sqrt{2}}$. Such a path would move alternately between corners and faces, but as there are $8$ corners and only $6$ faces, so this is impossible. So at least one of the edges must join to corners, and so the shortest length is $1+6\sqrt{2}$.