Partitioning revisited
We can show that (x + 1)² = x² + 2x + 1 by considering
the area of an (x + 1) by (x + 1) square. Show in a similar way
that (x + 2)² = x² + 4x + 4
Age
11 to 14
Challenge level
Problem
We can show that $14^2 = 196$ by considering the area of a $14$ by $14$ square:
We can show that $(x + 1)^2 \equiv x^2 + 2x + 1$ by considering the area of an $(x + 1)$ by $(x + 1)$ square:
Image
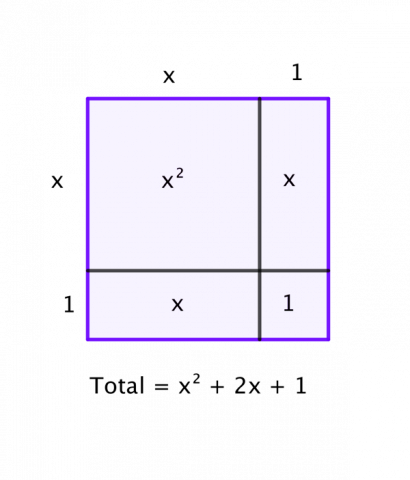
Show in a similar way that $(x + 2)^2 \equiv x^2 + 4x + 4$.
Then use the same method to evaluate $(x + 3)^2$ and $(x + a)^2$.
Getting Started
You may like to evaluate $(x + 4)^2, (x + 5)^2, (x + 6)^2$... before proceeding to $(x + a)^2$.
Student Solutions
Well done to all of you who answered this correctly. Unfortunately we cannot mention all of you here. A particularly clearly presented solution was sent in by Amir and James of Devonshire Primary school .
Teachers' Resources
A possible start to work on the expansion of brackets in algebra.
It enables students to make links with shape and space and with arithmetic.
A useful follow-up to this problem could be Multiplication square and Cubes within Cubes revisited