Circles in circles
Problem
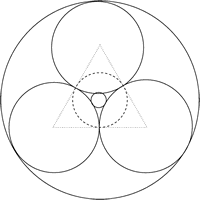
Take three unit circles, each touching the other two. Construct three circles $C_1$, $C_2$ and $C_3$, with radii $r_1$, $r_2$ and $r_3$, respectively, as in the figure below. The circles that are tangent to all three unit circles are $C_1$ and $C_3$, with $C_1$ the smaller of these. The circle through the three points of tangency of the unit circles is $C_2$. Find the radii $r_1$, $r_2$ and $r_3$, and show that $r_1r_3=r_2^2$.
Getting Started
Draw lines through the centres of the circles. Write down and solve some simple equations involving the radii. Remember to use the exact values involving square roots (irrational numbers).
Student Solutions
This solution together with the diagram was sent in by Derek Wan, age 17 of Sha Tin College, Hong Kong
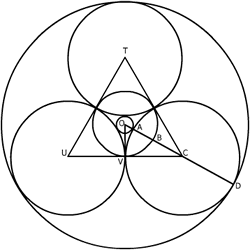
To find $OA=r_1$, $OB=r_2$ and $OD=r_3$ we must examine the diagram and make appropriate considerations. By dropping a perpendicular from $O$ to $V$, the midpoint of $UC$, as the radius is perpendicular to the tangent, we can find $OA = r_1$. Since triangle $TCU$ is equilateral $\angle TCU=60^o$ and $OC$ bisects $\angle TCU$ so $\angle OCV = 30^o$.
Since $OC=OA+AC$ $${CV\over OA+AC}={\sqrt 3 \over 2}$$ As $AC=CV=1$ and $OA=r_1$, $${1\over r_1+1} = {\sqrt 3 \over 2}$$ $$r_1+1 = {2\over \sqrt 3}$$ $$r_1 = {2\over \sqrt 3}-1$$ With $r_1$ we can find $r_2$ and $r_3$. Since $OV=r_2$, $CV=1$ and $\angle OCV=30^0$, $$r_2={1\over \sqrt 3}.$$ Since $OD=OA+AC+CD$, $$r_3={2\over \sqrt 3} - 1 + 1 + 1 = {2\over \sqrt 3} + 1.$$ Now $$r_1r_2 = \left({2\over \sqrt 3 }- 1\right )\left({2\over \sqrt 3} + 1\right )$$ $$\quad = {4\over 3} + {2\over \sqrt 3} - {2\over \sqrt 3} - 1$$ $$\quad = {1\over 3}$$ $$\quad = \left({1\over \sqrt 3}\right)^2$$ $$\quad = r_2^2$$
Teachers' Resources
This problem was studied by Descartes and the configuration is called 'Descartes' circles'. The ratios relate to equilateral and 30-60-90 triangles.
