The Medieval Octagon
Problem
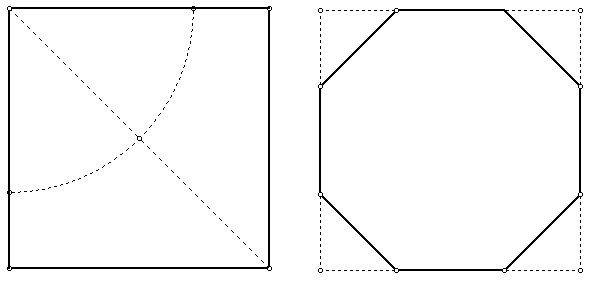
Medieval stonemasons used this method to construct exact octagons in a given square window.
Open your compasses to a radius of half the diagonal of the square and construct an arc with centre one vertex of the square - mark the 2 points where the arc crosses the sides.
Do that for all 4 vertices of the square giving 8 points which are the vertices of an octagon. Is the octagon an exact regular octagon? You may wish to explore using the GeoGebra applet below.
Move the slider to rotate the yellow square. Does this help you to prove that the octagon is regular?
Student Solutions
Solution by: Andrew Ross from Dr. Challoner's Grammar School
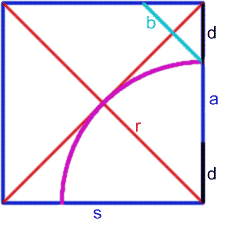
Call the side length of the square $s$. Use the diagram for other lengths.
The octagon has side lengths $a$ and $b$.
By Pythagoras' Theorem: $$r = {s\sqrt 2\over 2}$$ Because $s = r + d$ so $$d = s(1 - {\sqrt 2 \over 2}).$$ One side of the octagon is given by: $$a = s - 2d = s - 2s(1 - {\sqrt 2 \over 2}) = s(\sqrt 2 - 1).$$ By Pythagoras' Theorem $ b^2 = 2 d^2$ so $b = d \sqrt 2$. Hence $$b = s\sqrt 2 (1 - {\sqrt 2 \over 2}) = s(\sqrt 2 - 1) = a.$$ The octagon has rotational symmetry of order 4 as it was constructed from a square and all the sides are the same length, so it is a regular octagon.
