Penta Colour
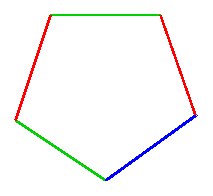
In how many different ways can I colour the five edges of a pentagon so that no two adjacent edges are the same colour?
Problem
In how many different ways can I colour the five edges of a pentagon red, blue and green so that no two adjacent edges are the same colour?
Student Solutions
Different interpretations of the problem led to different solutions from Caroline and Catherine of The Mount School, York; Matthew of Belfast Royal Academy; Gareth, James, Rachel and Sonya of Hethersett High School, Norwich; Helen of Madras College, St Andrew's; Chen Tu of St Peter's College, Adelaide, Australia and Kayleigh of Maidstone Girls' Grammar School.
Gareth, Chen Tu and Kayleigh included rotations and reflections as different solutions and used tree diagrams to show the 30 different possibilities. Practically speaking this is the answer; if you had a room with five walls then you could paint them 30 ways according to these rules.
First of all you start with either red, blue or green and use two different colours for the second side and so on around the pentagon. When you get to the last side it cannot be the same as the fourth side or the first one. You can do the same for green and blue in side 1 position.
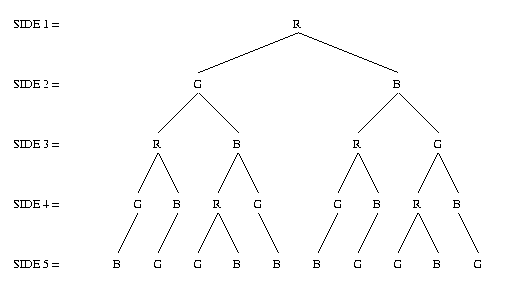
Gareth listed 6 different arrangements saying that all the others are rotations by changing the position of the single colour and Sonya, Rachel, James and Helen gave this answer.
BRGRG
BGRGR
RGBGB
RBGBG
GBRBR
GRBRB
Matthew, Caroline and Catherine went further to say that there are 3 ways because, with each single colour, the two colourings are reflections of each other.
