Is There a Theorem?
Problem
Imagine a square with sides of length $10$cm. This square will be fixed: think of it as being glued to the page.
Imagine a second square, of the same size, that slides around the first, always maintaining contact and keeping the same orientation.
In the interactivity below, the second square is red. It has a dot on its top left hand corner.
How far does the dot travel before returning to its starting point?
Try to predict the distance before using the interactivity to check your answer.
Change the position of the dot.
How does this affect the distance travelled by the dot?
Change the size of the second square.
What can you now say about the distance travelled by the dot?
Try the same problem with triangles or hexagons instead of squares
(remember your second shape is not allowed to rotate, or overlap with the original shape).
What happens if there are two different shapes?
Is there a theorem here?
Here are two related problems you might like to take a look at:
Rolling Around
Rollin' Rollin' Rollin'
Student Solutions
In the case of the two squares of side length 10cm, the dot travels 80 cm and the position of the dot does not matter.
Trying the same problem with other shapes leads to the following conjecture.
For any two shapes, the first in a fixed position and the second having fixed orientation; if the second shape slides around the first, maintaining contact then the distance travelled by any point on the second shape is the sum of the perimeters of the two shapes.
We show this in three further examples.
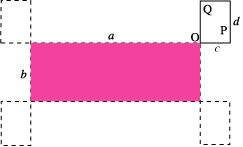
Consider two rectangles as in the diagram above. For any two points P and Q, the location of Q relative to P is fixed throughout the motion and so the distance travelled by P is the same as the distance travelled by any particular point that you choose, so we shall choose the point O, the bottom left hand corner of the moving rectangle . The point O moves a distance 2( a + b + c + d ).
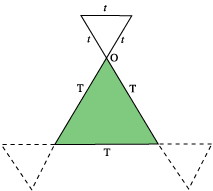
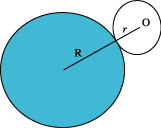
A similar argument holds for the triangles and circles shown below, choosing the marked point O in each case. The distance travelled is the sum of the perimeters of the two shapes; you can test this with other shapes!
| Distance travelled is 3t +3 T | Distance travelled is 2$\pi$( R + r ) |
Image
|
Image
|
