How old?
Cherri, Saxon, Mel and Paul are friends. They are all different
ages. Can you find out the age of each friend using the
information?
Age
7 to 11
Challenge level
Problem
Cherri, Saxon, Mel and Paul are friends. They are all different ages: $5, 6, 7$ and $8$ years old.
Image
Can you find out the age of each friend?
Use these clues to help you:
Mel and Paul's ages added together are double Saxon's age.
Mel's age is half of Cherri and Saxon's ages added together.
Mel and Paul's ages are both odd numbers.
Getting Started
Use the grid below to help you keep track of your answers as you follow the clues.
Image
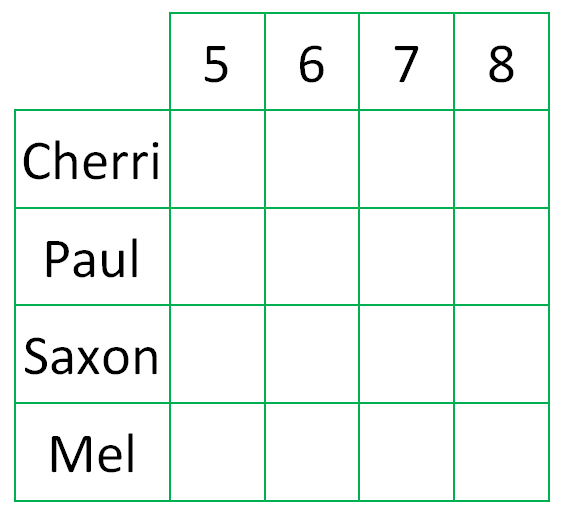
Which piece of information is most useful to start with?
How old is Cherri?
How old could Saxon be?
Teachers' Resources
How Old?
Cherri, Saxon, Mel and Paul are friends. They are all different ages: $5, 6, 7$ and $8$ years old.
Image
Can you find out the age of each friend?
Use these clues to help you:
Mel and Paul's ages added together are double Saxon's age.
Mel's age is half of Cherri and Saxon's ages added together.
Mel and Paul's ages are both odd numbers.
Why do this problem?
This problem requires children to practise basic number operations as well as working systematically. It encourages children to use some trial and improvement to work out what possible options there are and to reason about what the outcome of these different options would be. Choosing which clues to use in which order will help pupils learn how to organise information, identify redundant information and check their work.Possible approach
As a class, discuss the solutions to these questions, ensuring that pupils are confident with the wording of the problem:"Hollie is 9 and Tom is 11. Briony's age is half of Hollie and Tom's ages added together. How old is Briony?"
"George is 5 years old. Jess and Alfie's ages added together are double George's age. How old could Jess and Alfie be?"
Explain that in the case of the second question, we are interested in all the possible solutions. If we were also told that Alfie's age was an even number, what would the possible solutions be? What if we also knew that Jess was less than 4 years old?
Display the question about the four children's ages on the board, with the clues. Talk about possible approaches - what could be a helpful way to start? Some children might prefer to read all the clues first, whereas some might choose one to focus on and then move onto another clue. Encourage children to record their ideas and explain their reasoning to each other as they complete the task.
After pupils have solved this question in pairs, bring the class back together. Ask pupils to explain how they know they have the solution. Which information did they start with? Was any of the information not needed? Why?
Key questions
Which piece of information is most useful to start with?
Which pieces of information have we already used?
What age could that child be? Why?
What age can that child not be? Why?
Which pieces of information have we already used?
What age could that child be? Why?
What age can that child not be? Why?
Possible extension
Pupils could explain how they solved the problem, going through the order in which they used the pieces of information and why they used them in that order. What clues are not needed? What is the smallest number of clues that are needed to answer the question?
Children could then make up a similar problem of their own.
Children could then make up a similar problem of their own.
Possible support
Some pupils will find it helpful to have a table to use, as in the 'Getting Started' section.