Round and round the circle
What happens if you join every second point on this circle? How about every third point? Try with different steps and see if you can predict what will happen.
Problem
Round and Round the Circle printable sheet
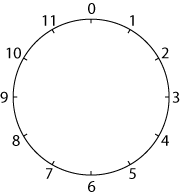
I started with a clock without hands or lines showing the minutes (except for those where there is a number). The $12$ was replaced by a $0$ and the numbers placed outside the face.
I drew straight lines to join up the numbers.
I started by counting in ones and I got a $12$-gon (that is a $12$-sided polygon - if you like long words you can call it a dodecagon).
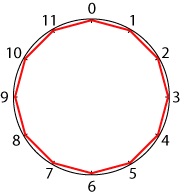
Then I drew straight lines counting round in $2$s. And I got ...?
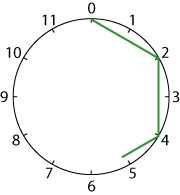
Perhaps you could try without putting the numbers round the circles.
I tried $5$s (wow!) and $6$s (well!).
Each time I go on drawing lines until I get to the point where I first started.
Then I tried $7$s, $8$s, $9$s, $10$s, and $11$s.
Something interesting was happening.
Why don't you try it? What patterns do you notice emerging?
And what about counting round in $12$s?
Which shapes are the same? Can you think of a reason why?
Can you see a connection between the number in which you are counting around the circle and the number of sides in the shape you are making?
Getting Started
You could use this sheet of circles marked in $12$s and this one that has circles marked in $10$s, $9$s, $8$s and $7$s.
You might find this interactivity helpful for drawing your shapes.
Student Solutions
From Mounts Bay School we had solutions in from Jamie, Luke, Cory, Luke, Joseph, Ben, Kara, Merrion, Katie, Ben, Chris, Ellen, Emma, Liam and Heidi. Here are three of them;
Certain numbers are the same. I think that numbers which are half of another number have double the amount of trails around the circle. This happens because when you try the numbers $8$ and $4$ they are exactly the same.
In the middle of each shape there is a perfect square. We can tell it is a perfect square because the angles are all right angles. We all figured it out together by looking and trying to do a number $8$ when we noticed the squares. We did not think it was a coincidence!
$12$ is equal
$11$ is the same as $1$ except backwards
$10$ is the same as $2$ except backwards
$09$ is the same as $3$ except backwards
$08$ is the same as $4$ except backwards
$07$ is the same as $5$ except backwards
$06$ is just a recurring straight line
All others are in reverse.
The pattern is that as the numbers from $11$ go down, the numbers which they are the same go up.
At the very end of the month we had two comments in from Morgan, Sara, Billie and Lucy from Southam St. James Primary School:
If the number of points are prime, all numbers will work but if the number of points are not prime all numbers apart from factors of the number of points will work.
and
If there's an even number of points odd numbers of steps won't work. If there's an odd number of points even steps won't work. If there's a prime number all of them work.
Teachers' Resources
Round and Round the Circle
I started with a clock without hands or the minute divisions (except for those where there is a number). The $12$ was replaced by a $0$ and the numbers placed outside the face.
I ruled lines joining up the numbers.
I started by counting in ones and I got a $12$-gon (that is a $12$-sided polygon - if you like long words you can call it a dodecagon).
Then I ruled lines counting round in $2$s. And I got .....?
Perhaps you do not need to put the numbers round the circles.
I tried $5$s (wow!) and $6$s (well!).
Each time I go on drawing lines until I get to the point where I first started.
Then I tried $7$s, $8$s, $9$s, $10$s, and $11$s.
Something interesting was happening.
Why don't you try it? What patterns do you notice emerging?
And what about counting round in $12$s?
Which shapes are the same? Can you think of a reason why?
Can you see a connection between the number in which you are counting around the circle and the number of sides in the shape you are making?
Why do this problem?
This problem brings out patterns in numbers, factors and multiples as well as properties of shapes. There are plenty of opportunities for visualising to predict what patterns will emerge. Learners will need to work systematically and to generalise, and the work done also often makes a very appealing 'finished product' for display purposes.
Possible approach
Key questions
Can you see a connection between these two numbers and the number of divisions round the circle?
What is the connection between these two numbers?
Possible extension
After doing the $12$s and $10$s, learners could try to predict which shapes will be produced with other numbers on the circle before testing their predictions. They could work on this sheet of circles divided into 10s, 9s, 8s and 7s. You might be able to introduce the concept of 'co-prime'.
Possible support