Tri.'s
Problem
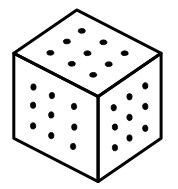
Many schools that I have worked in, which is quite a lot, have used nail boards with elastic bands to do some work on shape. Sometimes they have some plastic ones which do the same job and are less painful when you lean on them. Well this challenge is to use an idea that started with using nailboards like these but has changed into using 9 dots arranged in a square to be like a small 3 by 3 nail board.
If you use three lines, (like you may have had three elastic bands for a nail board) see what triangles you can make just using these nine dots. The lines MUST go from dot to dot, (like an elastic band has to go from nail to nail).
| The recording of these can get very confused so I suggest that you draw each new triangle on a new set of 9 dots. There are some to print off here . | Image

|
Image
|
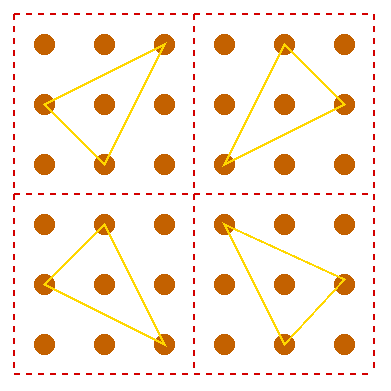
One thing which makes this challenge a little different is that if you produce the same shaped triangle but place it in a different position on the 9 dots then it can be counted as being different. |
| Notice also that there are some triangles that you can make
that do not have their vertices (corners) on the dots but they
still obey the rules:-
1) Use three straight lines only. 2) Each line must go from a dot to a dot. 3) You can only use these 9 dots arranged as shown. |
Image
|
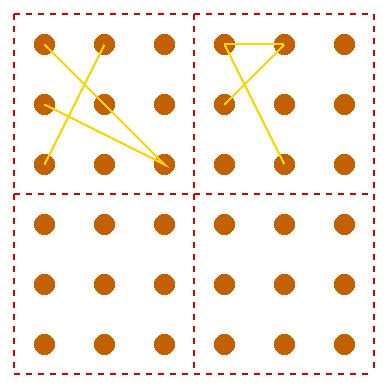
Well now, what about the smallest one?
Have you used any kind of system to get all the ones that are the same shape but put in different places?
How many of each triangle have you found?
Finally, the usual question for you to ask, "I wonder what would happen if ...?"
Don't forget to send in solutions and ideas and things that you have found out.
Getting Started
You might find it useful to print off this sheet of blank 3 by 3 grids.
Alternatively, you could use a virtual geoboard.
You could try drawing all the triangles you can from one spot to start with.
Student Solutions
There are lots of answers to this, depending on what questions you choose to ask. Here is what a teacher from Tudor Grange Academy Solihull wrote:-
Attached is my copy of as many answers to the Tri's task as possible. I used it with a year 8 class to get them to practice measuring angles, and to get them doing more problem solving and thinking laterally as part of my angles scheme of work. I got them to compete to see who could find the most different solutions, then got them thinking about whether the triangles were scalene, isosceles, right-angled, thinking about why none of them were equilateral, which of them were right angled, and discussing why using a protractor to measure the angles can be much less accurate than using mathematical methods to calculate the exact angles.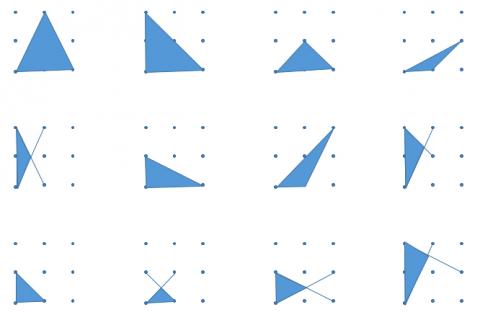
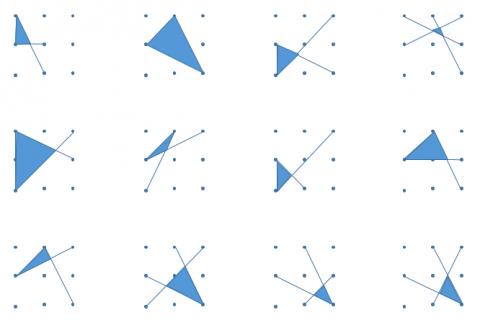
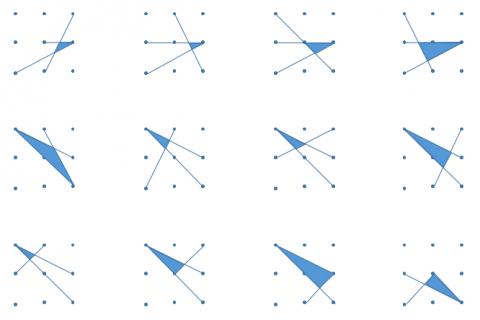
Thanks a lot for those they're great and show some good signs of creativity.
Have a go yourself, and if you discover anything interesting then email primary.nrich@maths.org. Please don't worry that your solution is not "complete" - we'd like to hear about anything you have tried. Teachers - you might like to send in a summary of your children's work.
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension
For more extension work