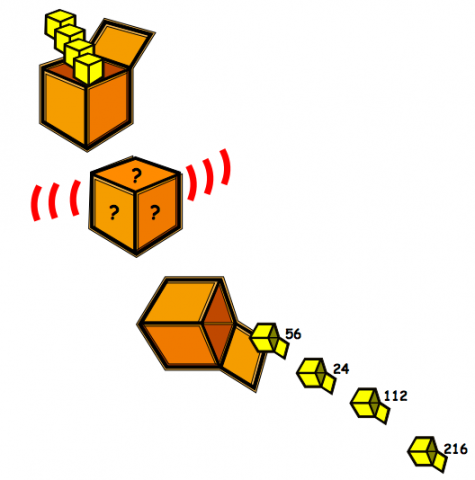
What's in the Box?
This big box multiplies anything that goes inside it by the same number. If you know the numbers that come out, what multiplication might be going on in the box?
Problem
What's in the Box? printable sheet
In the picture below, four whole numbers are being put into the box. Inside the box, a multiplication happens to each number, and then four new numbers are tipped out of the box: 56, 24, 112 and 216.

What multiplication might have happened to each number inside the box to get the answers in the picture above?
Are there any other possibilities?
What's the largest number that each of the four starting numbers might have been multiplied by inside the box? How do you know?
-----------
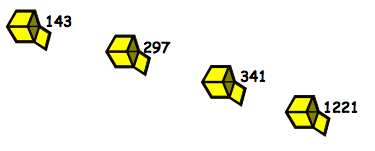
Imagine that four more numbers are put into the box, but now the box multiplies all of them by a new number. The numbers that come out of the box are:
143
297
341
1221
What number might the box be multiplying by? How do you know?
Discuss this with some other people and see if there are any different ways to work this out.
Getting Started
Remember, each of the four numbers that goes in is multiplied by the SAME number in the big box.
So, what is special about the four numbers that come out at the end?
Why don't you try out some ideas to see whether they work?
Student Solutions
We had a good number of solutions sent in with explanations as to how the answers were found. Ansh from Monkfield Park Primary School sent in the following:
For question 1) Answer is 8.
First of all I thought that 7 times 8 will be 56. Then I tried 3 times 8 and that also worked. Next I tried 13 times 8 that was 98 but that did not work so I tried 14 times 8 which was 112 and it was correct. Finally I divided 216 by 8 and ended up with 7.
So that's how I figured out that the multiplier is 8.
For question 2) Answer is 11
First of all I tried 3 and that did not work so I tried 6 and that did not work either. I also tried 7 and 9 but they both were wrong too. I knew it was not an even number so I skipped 2 and 10. Then I tried 11 and that worked.
So the first one was 13 times 11 = 143.
Next I divided 297 by 11 and the answer was 297.
After that I tried 341 divided by 11 and came up with 31.
Finally I did 1221 divided by 11 which gave me 111.
So the multiplier was 11.
Delaney at Mount Vernon School Maine, U.S. said:
Question 1 Possible factors: 2, 4 or 8
Largest common factor: 8
$56\div2=28$, $28\div2=14$, $14\div2=7$
$24\div2=12$, $12\div2=6$, $6\div2=3$
$112\div2=56$, $56\div2=28$, $28\div2=14$
$216\div2=108$, $108\div2=54$, $54\div2=27$
After I got these answers there were no more common factors and I assumed that 7, 3, 14, and 27 were the original numbers. 8 is the largest common factor because $2^3$ or 2x2x2=8.
Question 2 Only possible factor: 11
None of the numbers were even in this question so I knew that no multiples of two would be a common factor.
143=110+33
297=220+77
1221=1100+121
341=330+11
After dividing into portions divisible by 11, I found the original numbers by dividing by 11.
$143\div11=13$
$341\div11=31$
$1221\div11=111$
$297\div11=27$
There were no more common factors, so I assumed those were the original numbers.
We had this submitted from Jerry at Dulwich College, Shanghai:
First I checked which numbers that 143 can be divided by.
I skipped the multiples of 5 because 143, 297, 341 and 1221 clearly wouldn't be able to be divided by multiples of 5. I first found out 143 can be divided by 11 and 13. But 297 cannot be divided by 13. So I kept working on 11 and all four numbers can be divided by 11. So the winner is 11!

Well, altogether these have been very good responses to this challenge. Keep sending solutions to any other activity you have a go at.
Teachers' Resources
Why do this problem?
Of course this problem is rather like a function machine, but it can be more interesting for the pupils and easily extended to challenge a wide range of pupils. It could be used to introduce children to the idea of common factors and offers opportunities for learners to record in whatever way they choose.
Possible approach
It may be necessary to introduce the class to just one number going in and to give them one outcome to start with so that they understand the process. Then, gradually increase the number of numbers going in until you reach four, as in the problem. Your own examples can be adjusted in complexity according to the level of your pupils.
Once learners have had some time to work on the first part of the problem in pairs, ask them to share their ways of working with the whole group. Look out for those who give good reasons for choosing particular methods. At this stage, you could introduce the vocabulary of common factors if appropriate.
You may also wish to draw attention to interesting ways of recording. Some children may have drawn pictures, others may have written calculations and others may have done both.
Key questions
Possible extension
Pupils can be challenged to explain how they know they've found the largest possible number that the inputs have been multiplied by. Some pupils could go on to invent their own similar problems for others to do, including ones where a division is performed inside the box instead of a multiplication.
Possible support
Some pupils might benefit from beginning with the version of this task that uses addition and subtraction: What Was in the Box?
In order to introduce the multiplication version of this task, you can use sticks of cubes (such as multilink cubes) to represent one number going into the 'box'. Cover the cubes with a cloth and then secretly add the required extra number of cubes under the cover, in the form of more sticks of cubes, before revealing them to the child. Then a number of probing questions can be asked: How many cubes are there now? What has happened under the cover? Encourage pupils to consider how the number of sticks has grown, e.g. from 1 to 5, instead of simply counting how many more cubes there are.
As they tackle the main problem, some learners might find it useful to have a multiplication square or calculator available.
Money Bags
Problem
Ram divided $15$ pennies among four small bags.

He labelled each bag with the number of pennies inside it.
He could then pay any sum of money from $1$p to $15$p without opening any bag.
How many pennies did Ram put in each bag?
This problem is based on Money Bags from 'Mathematical Challenges for Able Pupils Key Stages 1 and 2', published by DfES. You can download a copy here.
Getting Started
How would you make $1$p?
What do you need to do now to be able to make $2$p?
Does this help to make $3$p?
Student Solutions
Harrison School sent in a solution from Charlie and Oscar as follows;
To begin, we decided to use post-it-notes as bags and sweets to represent our pennies - this made it easy to visualise the question. Then, we worked out that one could only be added to zero in order to make itself; there was now a bag with one penny in it. After that, we made a bag with two pennies in. We did think that we could make two with two ones yet that would give us a problem later. Next, we worked out that three could already be made using bags one and two. However, four could not be made with bags one and two, therefore we had to make bag three have four pennies in it. We then looked and saw we could make numbers five (bag one and three), six (bags three and two) and seven (bags one, two and three) but eight was unable to be made. Consequently, that means that eight has to be in bag four. This used up all the pennies - there were none left over. Finally, we checked that the numbers nine to fifteen worked, which they did. Nine = bags four and one. Ten = bags four and two. Eleven = bags four, two and one. Twelve = bags four and three. Thirteen = bags four, three and one. Fourteen = bags four, three and two. Fifteen = bags four, three, two and one.

Uma from Westhill Primary School, Aberdeenshire sent in her thoughts and the solution.
The solution for the Money Bags problem is 1,2,4 and 8 Here is the explanation of how I got my answer:
1p = Bag 1; 2p = Bag 2; 3p = Bag 1 + Bag 2; 4p = Bag 3; 5p = Bag 3 + Bag 1
6p = Bag 3 + Bag 2; 7p = Bag 3 + Bag 2 + Bag 1; 8p = Bag 4; 9p = Bag 4 + Bag 1
10p = Bag 4 + Bag 2; 11p = Bag 4 + Bag 2 + Bag 1; 12p = Bag 4 + Bag 3;
13p = Bag 4 + Bag 3 + Bag 1; 14p = Bag 4 + Bag 3 + Bag 2
15p = Bag 4 + Bag 3 + Bag 2 + Bag 1
Mr Howes' Magnificent Maths Group from Pierrepont Gamston Primary School
As part of an intervention group, we were a little confused to start off with - we didn't realise that the question was asking us to split the money into four bags so that the bags' totals could be combined to make any value up to 15p. Once we worked this out we wrote the values 1p to 15p down the side of the page and tried to find a system to solving the problem.
1p = this was easy, it had to be made with a bag with 1p in it!
2p = this could be made by another bag having 1p in it, or a second bag having 2p in it. We went for the latter because it stopped us using up our bags too quickly!
3p = this was also easy: 1p+2p
4p = We could either have another 1p or 2p bag, or a new 4p bag. We used the 4p bag.
At this point we spotted a pattern - 1p, 2p, 4p... would the next bag contain 8p?
5p = 4p+1p; 6p = 4p+2p; 7p = 4p+2p+1p; 8p = We stuck to our prediction and put 8p in the final bag!; 9p = 8p+1p; 10p = 8p+2p; 11p = 8p+2p+1p; 12p = 8p +4p; 13p = 8p+4p+1p
14p = 8p+4p+2p; 15p = 8p+4p+2p+1p
We thought that if the pattern was continued, the next bag should contain 16p ( making the total value 29p).
We wondered if this would be a better system for the values of coins; however, we realised that the values we used help us add up the numbers mentally much faster and make finding change easier!
James, Elliot, Freddie, Anna, Orla and Oliver
Jake from Duke of Norfolk School said
We drew out circles to show the different bags.
We tried to make all the numbers from 1 to 15, and recorded the number of pennies used in the circles.
We started with 1, 2, 3 and 5 coins, but found that we could not make numbers up from 12. We realised that we had to keep 1 and 2, because they were needed to pay 1p and 2p. So we added coins to the other bags, eventually settling on 1, 2, 4 and 8.
Stuart from Dussindale Primary School sent in this work and a good picture illustrating the solution
I started to look at multiples of ten but then realised I needed to use doubles/halves.
My first pair were 2 and 8 and then I saw I needed to have 1 and 2 and 4 and 8.
I used the cubes to make sure that I could make all the numbers from 1 to 15.

A Y4 maths group from Cabot Primary School, Bristol (Iman, Andrea-Marie, Sakariya and Aisha) worked on this problem together.
First of all, we found 15 play coins and a painting tray to help us think about the investigation and find a solution to the maths problem.
Secondly, we decided that we definitely needed to have one bag with 1p in it (or we would not be able to pay for something that cost 1p!), so we put 1p in one of the pots.
Then we thought about which numbers could make all of the other prices up to 15p. We realised that if we also had a bag with 2p in it, we could make 2p and 3p (1p + 2p), so we put 2p in our second pot. We tried 3p in the third pot and this gave us more prices:
1p (1p); 2p (2p); 3p (3p); 4p (3p + 1p); 5p (3p + 2p); 6p (3p + 2p + 1p)
...but we couldn't make 7p.
So we tried again, this time with 4p in the third pot. We could then make all of the prices up to 7p.
1p (1p); 2p (2p); 3p (2p + 1p); 4p (4p); 5p (4p + 1p); 6p (4p + 2p); 7p (4p + 2p + 1p).
We only had one empty pot left, so we put all of the rest of the coins into it - there were 8 of them. We then found that you could make all of the other numbers:
8p (8p); 9p (8p + 1p); 10p (8p + 2p); 11p (8p + 2p + 1p); 12p (8p + 4p); 13p (8p + 4p + 1p); 14p (8p + 4p + 2p); 15p (8p + 4p + 2p + 1p)
So we knew we had found the solution! We tried all the possibilities and didn't give up because Cabot Primary children are resilient! PS Our paint tray actually has six pots in it. We can see a pattern building up and are now going to think about how to investigate the maximum number of prices we can make if we use all six pots.
Later Sarah wrote and sent in this;
When we looked again at the number of coins in each pot, we noticed that each number was double the previous one. Since double 8 is 16, we put 16 coins into the next empty pot so we had five pots containing 1p, 2p, 4p, 8p and 16p. We knew the maximum price we could now pay would be 31p (our existing 15p plus the extra pot of 16p). We checked that we could now make all of the prices from 15p to 31p (which we could - by adding the new pot of money to each of the combinations that we had already found). We knew that we had found a system and that the sixth pot should therefore contain 32p (which is double 16p) and that we would be able to make all of the prices up to a maximum of 63p.
We then came up with this sequence to show how much money twelve pots (two paint trays) would contain:
1p, 2p, 4p, 8p, 16p, 32p, 64p, £1.28, £2.56, £5.12, £10.24 £20.48
It was good to hear about the different ways that solutions were found. Well done all of you.
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension
Possible support
School fair necklaces
Problem
Rob and Jennie were making necklaces to sell at the school fair.
They decided to make them very mathematical.
Each necklace was to have eight beads, four of one colour and four of another.
And each had to be symmetrical, like this.

How many different necklaces could they make?
Can you find them all?
How do you know you haven't missed any out?
What if they had 9 beads, five of one colour and four of another?
What if they had 10 beads, five of each?
What if...?
Getting Started
How will you record what you've found out? You might find it helpful to print out this sheet and to use colouring pens or pencils.
Is there any way of making sure you have them all?
If you cut out individual necklaces from the sheet, you can move them around and arrange them, which might help you find out if any are missing.
Student Solutions
We had a number of solutions sent in. Most treated the bracelets as being in a straight line rather than in a circle, which can make it more difficult to check whether you are duplicating ones already found.
We had the following from Lyneham Primary Junior Maths Challenge Group in Australia:
On Friday we worked on the necklaces problem in our maths group.
We used some different coloured counting blocks (unifix) to make symmetrical patterns of eight blocks with two colours.
We figured out that with those blocks we could make six different combinations that were symmetrical (see picture). And then we figured out that it didn't matter if you cut half of it off because they are symmetrical, so the halves are exactly the same.
We found six different towers of four blocks, two of each colour (see at the bottom of the photo). So therefore there are six possible ways you can do it.
We also heard from Cole and Sachi at Randlay Primary School:
I used O,G,G,O,O,G,G,O* for number one.
For number two we did O,G,O,G,G,O,G,O.
Number three: G,O,G,O,O,G,O,G.
Number four we did O,O,G,G,G,G,O,O.
Number five: G,G,O,O,O,O,G,G.
*O stands for orange and G stands for green.
We found over five ways to do the challenge that were different and symmetrical with the same colour.
I wonder whether you can see the sixth way that you've missed out?
Lara-Jade at Bay Primary School wrote:
I started with nine beads and worked out that because it has to be symmetrical the bead at the bottom must be of one colour because the clue says four beads of one colour and five beads of the other colour. So I thought yellow could be at the bottom and my pattern was:
Y,G,Y,G,(Y),G,Y,G,Y.
Then I worked out 13 beads. I thought because it is another odd number the bead at the bottom must be the colour of bead with the most in it. So I worked out the pattern which was
Y,G,Y,G,Y,G,(Y),G,Y,G,Y,G,Y.
Then I tried to work out what 10 was. Then I tried it and thought that it wouldn't work because it was even but I was wrong. So I tried it again and got the pattern right which was:
Y,G,Y,G,(Y)(Y),G,Y,G,Y.
I then moved onto 12. Because 10 worked 12 MUST work so I worked out the pattern which was: Y,G,Y,G,Y,(G)(G),Y,G,Y,G,Y.
Finally, I did 11 beads. And worked out the pattern which was:
G,Y,G,Y,G,(Y),G,Y,G,Y,G.
We had an email sent in from a teacher in Oregon U.S.A. saying:
My students at Springwater Environmental Sciences School found there were zero combinations that worked if you used 5 beads of each colour. I have attached a few explanations.


The teacher later added :-
We spent two class periods looking for a pattern, but could not find one.
One of my students realized that odds and evens should be treated differently, and as a class, we found that multiples of 4 always work, but could not find a pattern of how they increased as you added more beads.
One student had a great idea to start with smaller numbers of beads and work up from there to see the pattern, so we started with one bead but we always either had equal or only one more bead than the other colour.
This task was a great follow up to the three colour block tower (https://nrich.maths.org/137) because the symmetry aspect really changed up the thinking.
Thank you, this was a later solution that was emailed in which dealt very well with the situation when having 10 beads and 5 of each colour. Well done!
Did you find any other ways of making symmetrical necklaces, I wonder? Is there anything general you could say about even and odd numbers of beads?
It's interesting to see the different ways of recording thinking - some of you using cubes, some of you using letters and some of you using squared paper.
If you have worked on this activity, then do send us your thoughts too.
Teachers' Resources
Why do this problem?
This low threshold high ceiling task offers opportunities for children to confirm their understanding of line symmetry, to appreciate why working systematically is useful, and be introduced, or develop for themselves, a proof by exhaustion.
Possible approach
This problem featured in an NRICH Primary webinar in March 2022.
Most children will find some practical apparatus useful for this activity. Beads and string are the obvious choice but can lead to frustration if threading and re-threading is time consuming. A better bet may be interlocking cubes which can be stuck together (and can always be threaded later to make a display) or other similar objects in two colours. If you don't have an IWB (or even if
you do) you may want to make some versions of the necklace on large strips of paper which children can hold up at the front for all to see.
Introduce the task and together with the children, generate a symmetrical necklace. Challenge them to work in pairs to find as many other symmetrical necklaces as possible using eight beads, four each of two colours. When they think they have found as many as possible, they can record them on strips of paper (you could use this sheet cut
into individual strips). Giving separate slips of paper as opposed to a single worksheet will mean the children will be able to arrange and rearrange them.
Can they now arrange the strips to help them to see whether they have found all the necklaces?
Whilst they are doing this, copy the results they have found onto the large strips and then invite children to come and hold them up at the front. Ask "Do we have them all? How do we know? How can we be sure?" Encourage individual children to come to the front and rearrange the strips by moving their classmates around.
The most usual reponse to this is that the necklaces fall into pairs, each the inverse of the other (RRBBBBRR and BBRRRRBB, for example). Point out that this helps us to know that there should be an even number of solutions, but it doesn't prove that we have found them all - there might well be another pair that we haven't found yet.
Give some time for the children to rearrange their own strips and if anyone thinks they have found a way to show that they have found them all, invite them to come to the front and rearrange the large strips. If no-one does, you mght want to leave the children for some time - or even ask them to take the problem home - before sharing the proof below.
Focus first on the strips that begin with a red bead.
Arrange them so that the second red bead is in position 2, then position 3 and finally position 4:
RRBB BBRR
RBRB BRBR
RBBR RBBR
This must be the full set of necklaces beginning with a red bead since the second bead has been placed in each of the three other places.
If there are three beginning with red, there must also be three beginning with blue.
This exemplification of every possible solution is known as 'proof by exhaustion'.
Key questions
Can you make another?
How are these different?
How are these the same?
How do you know that is symmetrical?
Is your pattern the same as ...'s?
Do you think there are any more? Why/why not?
Can you show me why you think you've got them all?
Possible support
For some children producing more than one necklace will be a challenge, and transferring a pattern accurately onto paper will also be difficult, but worthwhile. Support them in looking for the same pattern using different colour combinations, for example RGRGGRGR is the same underlying pattern as BYBYYBYB. Making generalisations like this is a very important part of thinking like a mathematician.
Possible extension
Some children will be very interested in justifying their claim that they have found all the possibilities. Listen to their explanations - this is a wonderful opportunity for them to reason mathematically, and is the beginning of understanding mathematical proof.
Once they have convinced you, offer them nine beads, five of one colour and four of another. What difference does this make? What about ten, eleven, etc? Can they state any rules about the number of beads they need to make a symmetrical necklace with two colours?
Dice in a Corner
How could you arrange at least two dice in a stack so that the total of the visible spots is 18?
Problem


So, in the first picture above there are $3$s at the bottom of the red dice and on the top of the middle green and there are $4$s on the bottom of the green dice and the top of the white dice. The numbers on the seven faces that can be seen are then added and make $21$.
In the second picture above there are $4$s at the left of the red dice and on the right of the green dice and there are $3$s on the left of the green dice and the right of the white dice. The numbers on the seven faces that can be seen are then added and make $23$.
Use your own dice (you could use two or three or more...)
What total have you made?
Can you make a different one?
How many different ones can you make?
Now for a challenge - arrange dice (using at least $2$ and up to as many as you like) in a line in the corner, so that the faces you can see add up to $18$ in as many ways as possible.
Each line of dice must be along or up a wall (or two walls). A line going up is counted the same as a line going along. Remember the dice must touch face to face and have the same numbers touching. The dice must be all in one line, so this arrangement below is not allowed:

Getting Started
Don't forget that the face which are touching must be the same.
How will you make sure your arrangements are all different?
How will you know you have found all the different ways?
Student Solutions
Well done to everybody who found ways to make 18 using these dice in a corner. Kiran, Eeraj, Igla, Hassan and Ze-shaan from Crumpsall Lane Primary School in England investigated ways of making 18 using two dice:



Well done for finding so many solutions with two dice! The final picture is slightly unclear but this represents the solution:
2 4
4 2 6
Harry and Jack from Canberra Grammar School in Australia found four possible solutions using three dice:




Take a look at Harry and Jack's full solution to see their thoughts on this problem.
We received a solution from another Jack at Canberra Grammar School in Australia, who sent in these solutions for four and five dice:

Jack said:
I cannot show all pictures because the file size is too big!
That's a shame, Jack! I think there's one solution that nobody has found so far (that isn't just a rearrangement of one of the other solutions). If anybody thinks they have found it, please email us.
Teachers' Resources
Why do this problem?
Possible approach
Demonstrate the rule of "like faces facing", and then move the dice around a bit so that the rule is broken and ask if it's okay. Put the dice in the arrangement in the pictures and clarify how the total is calculated.
Before setting the children off on the challenge itself, you could ask them to find the smallest and largest possible totals for a stack of three dice so that they become immersed in the context.
Key questions
Tell me about this . . . .
How did you decide on this approach to finding all the possibilities?
Possible extension
How many ways are there for the most popular total?
Can you use a spreadsheet to get the results by using formulae rather than just entering data?