Working With Higher Attaining Mathematicians
A little while back I ran about fifty residential courses for the most able pupils, two dozen children at a time. At the end of each course we sat round and shared how it was for them being in an ordinary classroom and how it was during the weekend. I have subsequently made use of all that I learnt from these experiences while working for NRICH and providing in-service. So, here are some words
that I hope may help you when working with the most able pupils.
They, the children, are all very different, just as most collections of children are, and so some generalisations apply but need to be accepted as approximate guidance. These pupils will soon be acquiring concepts, skills and knowledge beyond our own and that could be the main difference between them and the remainder of pupils we come across. But, just like all pupils they need to have time,
respect and encouragement from the adults around them. Like most pupils they differ in their abilities in different areas of mathematics. Very approximately I have found those who have a flair when it comes to dealing with numbers and patterns, (for example Consecutive Numbers), those who have an amazing skill when it comes to visualising, and general shape and space activities
(for example More Pebbles) ...
... and those who seem to have a great flair in problem solving in areas of mathematics that do not recognisably fall into numbers, patterns, shapes or measures (for example Tea Cups).

These pupils also have varying degrees of perseverance. They may have different things in their lives that they are particularly keen about. Their communication with adults may vary greatly.
From the point of view of teachers there may be the decision as to whether to advance the pupils to the next level or to broaden their experience at the level they are operating on at the moment. I always like to point out that moving pupils to the next level assumes that we fully understand all about pupil development in learning mathematics, backed up by what neuroscientists are telling us
about how the brain works and changes. (See 'What Counts - How Every Brain is Hardwired for Math' by Butterworth and 'The Number Sense - How the Mind Creates Mathematics' by Stanislas Dahearne.)
If we broaden out, they are much more in control of where they are going and they will indeed come across skills that are new and need to be acquired in order to go further. These skills can usually then be learnt quickly with a kind of injection, the need, being the driving force of solving a problem. The gaps in the pupil's knowledge and/or skills may not be what the teacher anticipates. Some
teachers have been anxious about doing open-ended/investigative work. They sometimes have felt that they are not prepared to try this work until they have taught all the aspects of knowledge and skills they think may be required. However it seems that the investigative approach gives pupils opportunities for constructive thinking and for acquiring skills and knowledge along the way.
Now we will look at some particular activities and other aspects of the learning environment that the teacher has the power to change.
Sometimes when there is a problem to be solved that is based on a 2D situation it's a call to ask "I wonder what would happen if this problem was transformed into a 3D situation?" (for example Tri.'s, Pebbles, Fencing).
Some pupils will be suitably challenged by being asked to communicate the way they got to a solution of a particular challenge either orally or in written form. When talking directly with pupils it's all too easy to promote your own ways of setting something out because you see a particular advantage in doing so. I learnt, early on in my teaching career, to hold back from these suggestions
because our ways of thinking may not be the pupils'. Also what we anticipated becoming a problem or difficulty may only be so for us and certainly not for that particular pupil.
I'd like to return for a moment to the point that pupils may excel at one particular area of maths and not others. So, some pupils who we see as the most able may only be so when it comes to one area of the subject. So, just as an example, we should not expect the child who excels at computation to necessarily by any good at visualisation. We should therefore be cautious with what we say when one
of these pupils comes up and says "I cannot do this at all!" A reply such as "But you are very good at maths, of course you can!" is not what is called for. A youngster on one of the 'able pupils' maths courses was telling us all about his worst moment of the previous week in school. He said, "I went up to my teacher and said I cannot do this. She turned to me and said 'yes you can, of
course you can, you're very good'." I turned to the boy and asked him how he felt at that moment. His reply was "I felt like a glass wall as if she had never seen me." Well it is very likely that the teacher thought she was complimenting him and it was a good thing to say. How very careful we should be. We will all make mistakes but it's good to get to know the children very well and
apologise to them when we get it wrong.
Some teachers will profess that one of the best ways of dealing with the most able is to get them to explain and help those who are not doing so well. Well, from what youngsters have said to me about that, it would seem that they do not mind it occasionally. Sometimes pupils of a high level have certain things at their finger-tips and can no longer explain the thinking behind it. Sending in
their solutions to NRICH activities can be one way of them communicating their thoughts, for a purpose.
More and more of the activities on this web site have, within the teachers' notes, a section named, 'for the most able' or 'for the highest attainers'. The intention here is that such extension work will give opportunities for those who are most able - probably the one you get every three or four years, who shows an exceptional talent and flair in the subject. 'Talent' and 'Flair', I believe are
essential words to use when talking about these most able pupils. They need to show certain perseverance in their particular area of mathematics I believe in order to be deemed most able. There are pupils in most classes that we would say are more able than the others but here we are talking about the one per cent or even fewer.
So, you are sitting with a very able pupil, you've been doing Tri.'s,
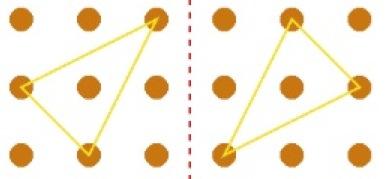
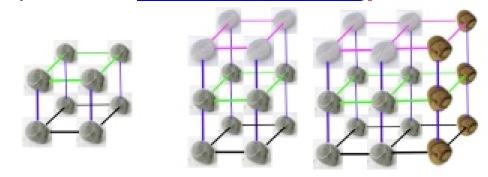
and s/he found it too easy so you go to the Teachers' Notes for that activity. Here you are given a brief idea as a starting point for challenging the pupil whose extra abilities lie in the field of visualisation in shape and space. You are unlikely to have a hollow cube with nine holes in each face so that's the starting point for imagination. The pupil then has to go about visualising the shape
that is generated inside the cube when they have passed three threads through the holes. You then might encourage them, if it seems appropriate (knowing the pupil well), to make a record of the triangles and how they were formed. If that also seems easy then, as suggested in the notes, they could move onto thinking about tetrahedrons. A really hard challenge, when several tetrahedrons have been
found, is to check that they are not the same. At an appropriate time, probably when you are thinking that perseverance is coming to an end, you might encourage them to ask "I wonder what would happen if I ...?"
Throughout the session with the pupil(s) the way the teacher communicates is of paramount importance. You are in the same kind of role as counsellors finds themselves with clients in 'Person Centred Counselling'. So there's a lot of deep listening and a few interjections of just a couple of words (yes, O.K., tell me more, etc.) with no rush and silences respected.
Here is a PDF version of this article.
