Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Magic Crosses
Age 7 to 14
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Well done to everyone who sent us a completed magic cross using 1, 2, 3, 4, 5.
Kristof from Moss Hall Junior School in the UK described a method for making a magic cross:
To find all possible magic crosses, a good technique is to think of numbers for a row. Then add the 1st and 3rd numbers but not the middle one. Then you find 2 numbers which also add up to that same number, but doesn't include any of the original 3 numbers. However, not all the ways to pick the [first] 3 numbers can make a magic cross.
Amelia from Slip End Village School in the UK sent in several similar crosses and an interesting comment:

This is a magic cross
I found it by moving numbers around



You could also do it like this but it is kind of cheating because I didn't change the middle numbers around
Notice that the 1 is always in the middle, the 5 is always opposite the 2, and the 3 is always opposite the 4. Does that mean Amelia is 'cheating' and they are all different versions of the same magic cross? Some people thought they were different crosses and others didn't.
Andrew from Island School in Hong Kong, Deana from Bangkok Patana School in Thailand, Iqra from Uphall Primary School and year 5 and year 6 at Tanners Brook Primary School in the UK tried putting different numbers in the middle.
Tanners Brook Primary School also considered the totals. Click here to see their work.
Andrew described a systematic approach:
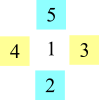
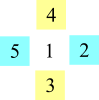 Working systematically, I tried finding different crosses with 1 as the middle number. There were
two magic crosses. I then tried to use 2 as a middle number. There was no magic crosses with 2 as a middle number. I hypothesized saying that the number in the middle needs to be odd in order for Magic Crosses to happen. Then I tried 3,4,5 and indeed, only 3 and 5 had magic crosses. My hypothesis was right. I also found that each middle odd number had 2 possible magic crosses however with the
numbers on each horizontal side of the number becoming the vertical side numbers (as shown above).
Working systematically, I tried finding different crosses with 1 as the middle number. There were
two magic crosses. I then tried to use 2 as a middle number. There was no magic crosses with 2 as a middle number. I hypothesized saying that the number in the middle needs to be odd in order for Magic Crosses to happen. Then I tried 3,4,5 and indeed, only 3 and 5 had magic crosses. My hypothesis was right. I also found that each middle odd number had 2 possible magic crosses however with the
numbers on each horizontal side of the number becoming the vertical side numbers (as shown above).Therefore there are technically 3 magic crosses as the other 3 is the same cross except for the numbers on the vertical side of the middle no. swapping with the numbers on the horizontal side of the number. (Andrew thinks that all of Amelia's magic crosses count as the same cross)
Libby, Isaac and Thea from Edward Bryant School, Amina, Fatimah and Yasmin from Castle Academy and Mr J's class from Banstead Prep School in the UK explained why you can't put an even number in the middle.
Edward made a video which explains this and some other concepts, which is here: https://youtu.be/9gsXurHs0V8
This explanation comes from Mr J's class:
We were not able to make magic crosses using 2 or 4 in the middle. These even numbers were not possible because you were left with three odd numbers and one even. We could not make pairs of numbers from these that were either two odds or two evens.
To make a magic cross, once you have removed/chosen your center number, you need an equal number of even and odd numbers remaining.
we found these crosses.
1 at the center = 2+1+5 and 3+1+4 (totals 8)
3 at the center = 5+3+1 and 2+3+4 (totals 9)
5 at the center = 1+5+4 and 3+5+2 (totals 10)
What about other crosses with the same number in the middle, which some people counted as different crosses?
Isaac said:
I realized that you can rotate the numbers on the outside around the one in the middle.
Amelia, Bea, Liadan, Hannah, Sophie and Lydia from Sandbach High School in the UK said
There are 8 different rotations or reflections for each different number in the middle.
Diya from International School of Brussels in Belgium sent in an image which explains how to find these 'rotations' and 'reflections'. Diya gets a total of 21: 3 rotations + 4 reflections, multiplied by 3 possible middle numbers. But Diya forgot the original unrotated version, so really there are 8 $\times$ 3 = 24. Click here to see Diya's work.
Iqra sent in some magic crosses using the numbers 2, 3, 4, 5, 6:
Shriya from International School Frankfurt in Germany sent examples for all of the sets of numbers given. Click here to see Shriya's first page and here to see Shriya's second page.
Owen and Jayseung from Dulwich College Beijing in China found all of the solutions using 2, 3, 4, 5, 6 using a method involving the median:
After experimenting for a long time, we found out that 2, 4, 6 are the only possible numbers in the middle if you do 2,3,4,5,6, because if you have 2, 4 or 6 in the middle, we will be able to pair up the leftover numbers so that their sum is the same.
After putting a number in the center (for example, 6), I lined up the 4 numbers from smallest to biggest (for example, 2 3 4 5).
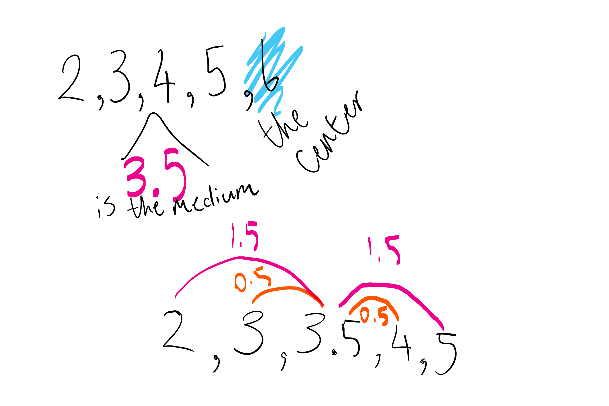 After that, I found the median, which is 3.5. The distance 3 has from 3.5 is the same as the distance 4 has from 3.5 (0.5) so they can be a pair. The same goes for 2 and 5 so they can be a pair and the center number won't affect the total as it will be the same for the horizontal and
vertical.
After that, I found the median, which is 3.5. The distance 3 has from 3.5 is the same as the distance 4 has from 3.5 (0.5) so they can be a pair. The same goes for 2 and 5 so they can be a pair and the center number won't affect the total as it will be the same for the horizontal and
vertical.Scout from James Allen's Prep School in the UK described how a magic cross can be generated from any 5 consecutive numbers:
I want consecutive numbers 12, 13, 14, 15 and 16. Here's a little trick:
1. Put the numbers into numerical order. (12, 13, 14, 15 ,16)
2. Put the middle number (median) in the centre of the cross. (14)
3. Take the smallest and largest and put them together in a column or row. (12,16)
4. Take the two numbers closest to the median and put them in any order in
the remaining places. (13,15)
5. You have made a magic cross! Works every time!
Egor, Fede and TJ from International School of Brussels in Belgium, Deana, Thea and Libby extended their earlier ideas to other sets of numbers.
Thea said:
The second problem used the numbers 2, 3, 4, 5 and 6.
There were 8 solutions adding up to 11, 8 solutions adding up to 12 and 8 solutions adding up to 13.
The numbers used were mainly even, meaning an even number had to be in the centre square.
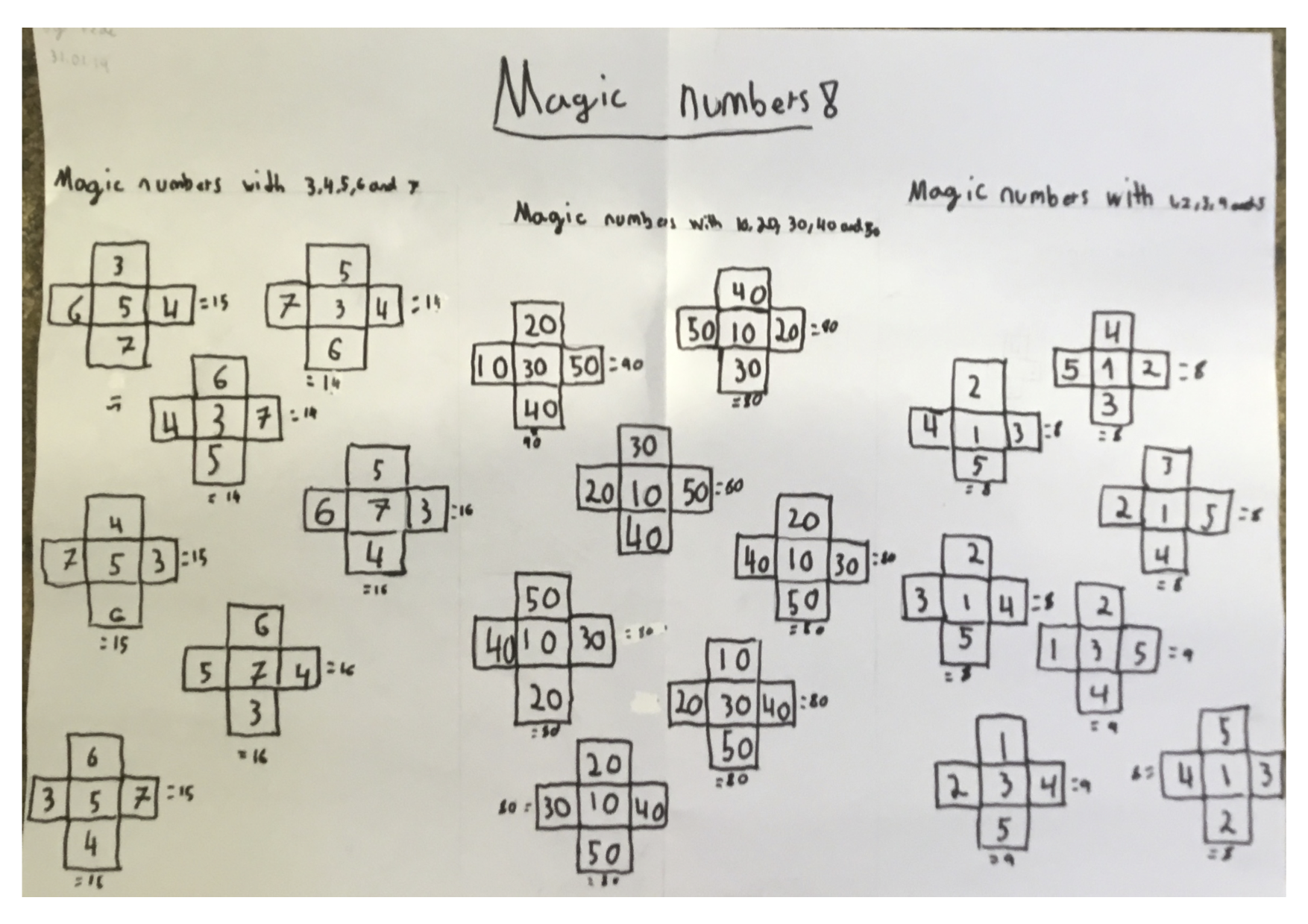
The third problem used the numbers 3, 4, 5, 6 and 7.
There were 8 solutions adding up to 14, 8 solutions adding up to 15 and 8 solutions adding up to 16.
The numbers used were mainly odd, meaning the number in the centre square had to be odd too.
Libby explained why if you only have 2 odd numbers, you can't put an odd number in the middle:
If you put an odd number in the middle, an odd number on top and an even number everywhere else (see picture a) it would not work because one answer is odd and one is even. When there are only 2 odd numbers, neither can fo in the middle.
It is the same with even (when there are 2 even numbers).
Deana found some numbers which could make magic crosses with the number 50 in the middle:
How many magic crosses can you find with the number 50 in the middle?
3 because if you need to find the number around it, which is
1. 50, 51, 52, 53, 54
2. 50, 49, 48, 47, 46
3. 50, 51, 52, 49, 48
Year 3 at Moulsham Junior School used numbers which were 10 apart. How are these crosses similar and different to the crosses using 1, 2, 3, 4, 5? Do you prefer the cross-representation, or the V representation?
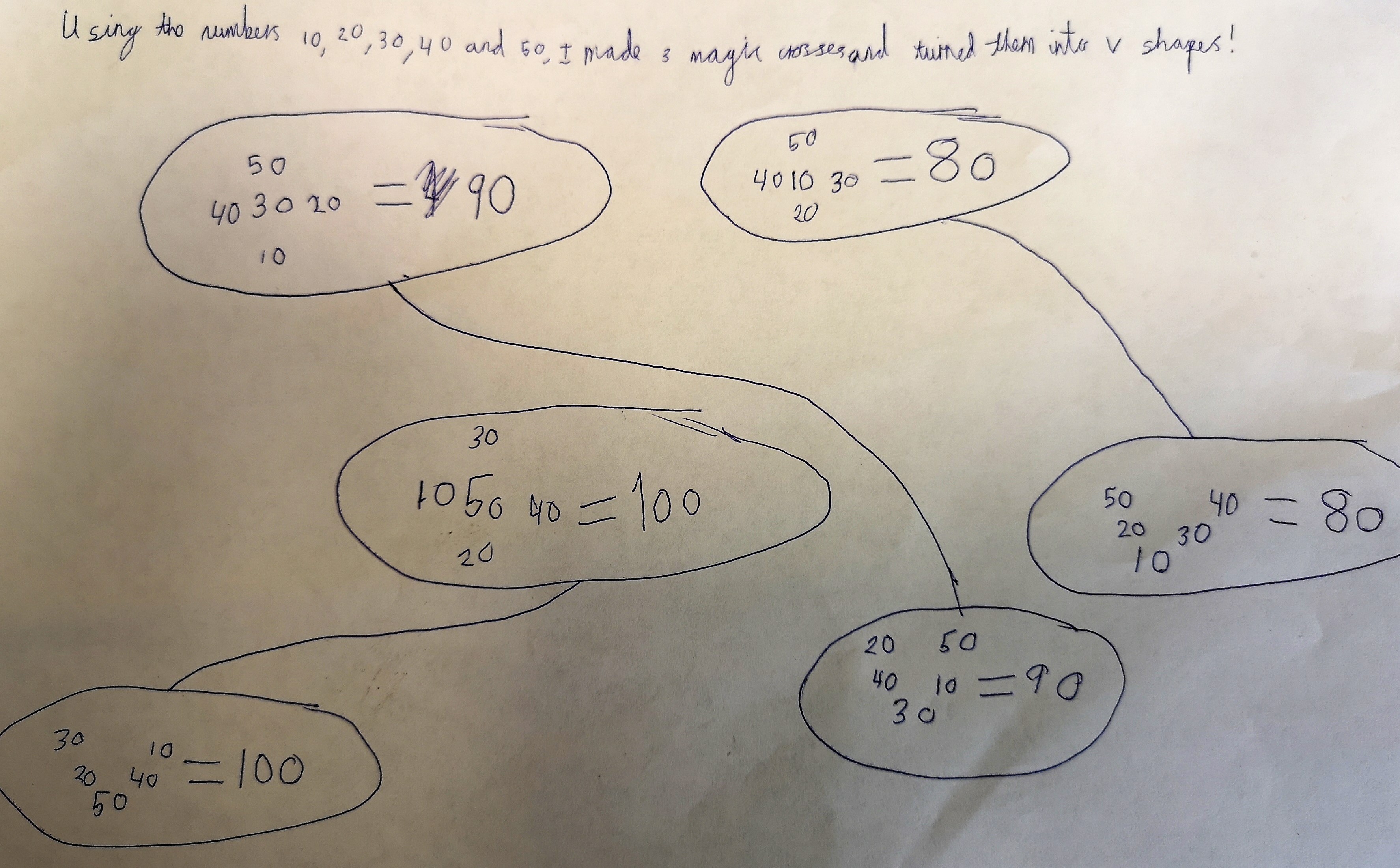
TJ described a new method and made some magic crosses with repeated numbers:
Click here for a larger version of the image.

Fede made magic crosses with lots of different sets of numbers:
Click here for a larger version of the image.
Egor explained how to make a magic cross with any 5 numbers:
Click here for a larger version of the image.

A last minute solution came in from St. Swithun's School (Winchester)the teacher sent in a word doc of Abigail's work which extended the task quite a long way. Here is part the whole doc can be viewed here .docx
There are eight ways to do it with one number in the middle. Even numbers can't go in the middle because there will only be one even number and three odd numbers. I did this with all the numbers, and I figured out that one, three and five were the only possible numbers in the middle and there were three of them. I then figured out that that two and four were not possible because of the even reason. I figured out that 3 x 8=24 and that there were 24 ways.
A solution came in from Rishi at Orton Wistow Primary School, here is one short sentence of a very thorough solution.
What I've noticed in these crosses is that the numbers in both crosses are from 1-5. I have also noticed that in both crosses the digit 4 and the digit 2 remain stationary in the two images.
Rishi's full solution can be viewed here.docx.

