Jennifer Piggott and Steve Hewson write about an area of teaching and learning mathematics that has been engaging their interest recently. As they explain, the word 'trick' can be applied to mathematical activity in many ways.
In this article we discuss the role of 'tricks' in mathematics, that they can be either simply misleading or content or process driven and how they can provide positive or negative experiences for the learner. The more we have thought about this the more we are aware that we have only scratched the surface of this issue, but we are sharing our early thoughts and hope it will elicit further discussion and refinement. Throughout we shall refer to mathematical content and mathematical process. You can think of the former as knowledge and the latter as skill.
In short, we want to explore the question: what is a mathematical trick and when are tricks good and when are they bad?
Focusing attention on tricks
Here are seven reasonably quick questions chosen to highlight various aspects of the word 'trick' in mathematics. As you try to solve them, do you see any part of their solutions as 'tricks'? Do you feel that you need to use a 'trick' to solve them? Why?
The solutions are available at the end of the article. It will be better to try the questions before looking at the solutions, as the way in which a trick is received by the learner is an important aspect of this article!
1. As I was going to St Ives, I met a man with seven wives. Every wife had seven sacks; And every sack had seven cats; And every cat had seven kits. Kits, cats, sacks, wives: How many were going to St Ives?
2. Find the missing term in this sequence: 110, 20, 12, 11, ... , 6, 6
3. Continue the sequence J, F, M, A, M, ..
4. Evaluate $\int^2_{-2}\left(x\cos(4x^2)+x^2\sin(4x)\right)dx$
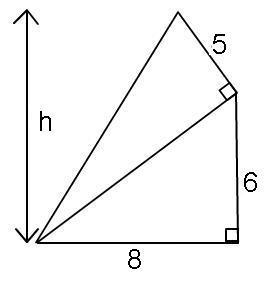
5. Without using a calculator, find the height h in the diagram below
6. Find $x$ if $x - 6 = 27 - 2x$
7. Find a pair of natural numbers the cubes of which differ by a million
Assessment of the problems
As we shall see, the word 'trick' might be applied to these problems in various ways. Although for each one we focus on a major point which arises, the range of issues uncovered are not mutually exclusive. In each case, we provide an example of 'positive' classroom use and an example of 'negative' classroom use. Positive uses might lead to improved understanding or enjoyment, whereas negative used might lead to frustration, mistrust or confusion.
Question 1 - Deliberately misleading the solver
This is the classic trick question: the question is specially designed to catch out and fool the solver. If you have seen this question before, recall or imagine seeing it for the first time. Imagine a youngster trying to solve the question by attempting to work out $1 + 7 + 7\times 7 + 7\times 7\times 7 + 7\times 7\times 7\times 7$ only to be told 'No. The answer is $1$. The others were coming away in the opposite direction'. How would such a learner feel? Despite looking mathematical, there is no mathematical content in the answer.
Positive use: Posed in a mathematically honest way to try to get students to convert a question into a written sum: the focus would be on the mathematical process rather than the answer itself. The 'trick' would then be a fun twist.
Negative use: Phrasing the question in a way which emphasises the combinatorial aspect or in a way in which people might start a long calculation, where the aim is to focus on catching out the solvers.
Question 2 - Could be a trick, depending on the context in which the question is received
To solve problem this you need to try to interpret the digits in different number bases. Is this a trick? It depends on the context in which the question is received. Consider it as part of a series of questions involving arithmetic sequences: in this context it would be a trick question, given out of context and designed to mislead. If it were given in the context of work on number bases it would take on a very different, positive character. Furthermore, if presented as a pure puzzle to challenge your thinking then it could also have positive benefits (what mathematics could I bring to bear that will help me solve this problem?). This problem immediately raises the issue that context is important in determining whether a question is a trick question or not. In short, were this question presented as a year 7 question or in a set of exercises on algebraic sequences this would be very misleading. Were it presented in the context of a set of A-level exercises on modular arithmetic, the problem would take on a very different flavour.
Positive use: To encourage creative engagement with number bases, or with a suggestion that the standard mathematical content for sequences will not work.
Negative use: With no hints that 'standard' methods of sequences will fail. Given to students who might understand number bases, but are unlikely themselves to think of number bases as a method of solution.
Question 3 - A question immediately solved only by spotting the answer
The answer to this sequence requires you to spot the pattern of months of the year. Is this pattern-spotting process a mathematical exercise? It is interesting to consider how it differs from the previous question. In question 3 there is some sense that there is virtually no calculation needed to solve the problem once the solver has made the connection with the months of the year, whereas in the question 2 a logical process needs to be undertaken to apply the idea of number bases. We make the point that this is a non-mathematical puzzle: the 'trick' can be applied instantly without calculation or recourse to mathematical reasoning of any sort.
Positive use: To encourage students that letters don't always need to stand for numbers
Negative use: Given in any situation in which solvers are expecting a numerical answer
Question 4 - Quick shortcut to a solution using an advanced mathematical procedure
This is the first question to sensibly allow multiple methods of solution. The answer could be derived at length by using integration by parts multiple times, but the mathematical trick of spotting that the integrand is odd allows you almost immediately to arrive at the answer. This is a mathematical process trick. This question could be posed negatively as a trick to mislead the solver into wasting time on a lengthy algebraic calculation, but the 'trick' to arrive immediately at the solution has a reusable quality to it: it is a trick that might well become a tool in future problem solving situations. We assume in this case that the problem would be used in a context designed to elecit the development of a useful mathematical tool rather than in circumstances which are misleading.
Positive use: The question could be used to provide some integration by parts practice with the interesting answer zero leading naturally onto the discussion of the clever trick which might be employed next time.
Negative use: Given to a mixed group of students for whom some will immediately spot the trick, whereas others will start working on integration by parts. Do the trick spotters sit around waiting, or do the integrators have their work interrupted by finding out the answer before they have finished their computation?
Question 5 - Neat shortcut using a simple mathematical process trick
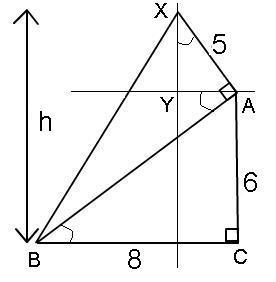
This problem allows for multiple methods of solution. One possibility is trigonometric which requires a calculator; another approach involves spotting firstly that the base triangle is a 6-8-10 Pythagorean triangle and secondly that a cunningly placed pair of lines allows you to use similar triangles to solve the problem. Using these lines feels like a trick because once they are in place the problem becomes much simpler. Placing additional lines on a diagram is a useful trick which could be applied to a wide variety of problems: it is a mathematical process trick. Whilst this trick does not immediately give rise to the answer, it does open up alternative avenues and raises the issue of elegance in a solution.
Positive use: Given to students who are likely, with enough necessary scaffolding, to be able to think of the trick of applying additional lines to the diagram.
Negative use: Given in any context in which students will become completely stuck.
Question 6 - Tricking the solver by using a misleading context
This question was placed towards the end to make you suspicious. Were we, the question setters, trying to trick you into giving the wrong answer? No. But hopefully this reinforces the point about the context in which a question is set leading to the attitude of the solver towards the problem. It also raises an addition point. To solve this equation you most probably mentally rearranged to get $3x = 33$ and then divided to get $x = 11$. But rearrangement of terms and then division are both in themselves tricks. Anyone who has ever taught algebra to a class of year 7 pupils will understand that, initially, such rearrangements and divisions are far from obvious for most pupils. They become mathematical content tricks, such as the integration trick in question 4 eventually becomes to more experiences mathematicians: to solve equations like these you can follow these steps
Positive use: Misleading contexts might be used to encourage learners to think outside the box.
Negative use: Used in a situation where solvers doubt their knowledge or ability to do the question, so that they feel suspicious of the question.
Question 7 - Quick solution using an advanced mathematical content trick
This is a misleading question because there are, in fact, no natural numbers the cubes of which differ by a million. A very quick way to see this is to note that Fermat's last theorem says that there are no whole number solutions to $a^3+b^3=c^3$. Since 1 million is the cube of $100$, we know that there is no possible whole number solution to the question. The trick is to use a theorem: without knowledge of the theorem the question is very difficult; with the theorem it is trivial. We can consider the theorem to be a mathematical content trick.
Positive use: Provided in a time-constrained way as an interesting introduction to a fascinating mathematical context.
Negative use: As an unsupervised homework task: students might, believing that there is an answer, spend a great deal of time working on the problem and failing to make progress.
Motivated by the discussion of the previous questions, we are now in a good position to try to categorise tricks in mathematics.
Categorising tricks in mathematics
Clearly, whether a question is received as involving in some way a trick very much depends on the way in which it is presented and the mathematical skill and knowledge of the solver. In fact, when writing this article we disagreed many times on whether a given activity constituted a 'trick', and came to realise that a trick very much depends on the learner and context. We concluded, however, that it is possible to provide a simple breakdown of tricks into three simple categories:
1. Trick questions
2. Questions which can be more quickly solved using mathematical tricks
a. Questions using mathematical process tricks
b. Questions using mathematical content tricks
Whether a question falls into category 1 depends very much on the context in which the question is presented. Whether a questions falls into category 2a or 2b very much depends on the mathematical level of the problem solver.
Discussing these categories more generally, away from specific examples, will allow us better to understand the purpose of such questions in mathematics learning. We do not attempt to provide a complete list or categorisation in this article; this might be the focus of further, more detailed investigation.
Trick questions
These are questions specifically designed to mislead the solver in some way, such as:
1. You are deliberately misled into creating a difficult answer or following a difficult path when there is a simple, immediate answer or route to the answer
2. You are misled into creating a simple answer when the actual answer is more difficult.
Trick questions can be made (intentionally or otherwise) by
1. Choice of misleading wording or notation
2. Choice of misleading context
3. Choice of underlying mathematics that the solver is unlikely to know or think of
A trick question is likely to result in the solver immediately seeing the solution upon being told the trick.
Why might you use a trick question? A main reason is to reinforce a learning objective (such as always read the rubric) or to make a lesson more memorable. However, be aware that tricking the solver can lead to either positive or negative emotional responses:
Positive: Intrigued, amused, motivated, full of wonder.
Negative :Embarrassed, foolish, irritated, angry
It is important to be aware that the right sort of trick at the right time can lead to a sense of delight, but the wrong sort of trick can confuse or embarrass the learner, create a sense of mistrust or defensive environment in the classroom.
Mathematical tricks
Clearly, a trick question can be created in any subject, including mathematics. However, many of our examples use 'mathematical tricks'
The best way to understand the use of a mathematical trick is to imagine that you are stuck on a problem and can find no way forward. You cannot start and then, suddenly, there is a light bulb moment and you can suddenly see how to proceed. You might on occasions be able to see your way immediately and obviously to the answer, or you might still need to do some work to process or apply the trick ' however, there is a definite 'ah!' as you realise how to proceed. At a most basic level, the light bulb is the trick and it jumps you from not knowing how to start to the problem to being confident as to how to proceed. Sometimes the trick will be a piece of firm knowledge, such as a theorem; at other times it will be a process of sorts, such as cleverly splitting up a diagram
In the example questions, the mathematical light bulb moments were
1. No mathematical trick
2. Thinking of applying different number bases
3. Thinking of the sequence of the months of the year
4. Realising that the integral was odd
5. Thinking to apply lines to the diagram
6. Realising that the equation can be rearranged
7. Spotting the connection to Fermat's last theorem
This list highlights the fact that mathematical tricks can be broken down into tricks of content and tricks of process. To be clear, mathematical 'content' is a piece of factual, mathematical knowledge, such as the definition of trig ratios; mathematical 'process' is the means and skill by which you use and apply your general mathematical content knowledge. In almost every mathematics lesson, students use, are made aware of, or even subjected to a range of mathematical tricks. Whether these are viewed as tricks largely depends on the familiarity of the learner to the mathematical ideas. Consider, for example, the familiar knowledge that there is a formula for the solution of any quadratic equation. Why might it be thought of as a trick? Imagine asking a non-mathematician to find a number which equals a quarter of its square added to 35/36. In a couple of moments, the mathematician can spot the quadratic equation and will soon find the exact answer. It is no surprise that ancient cultures held such knowledge in almost magical esteem! On a more day to day level, there is often an element of magic in the learning of new mathematics. Although this magic might fade over time teachers might do well to remember the mystery that new mathematics holds for their learners.
Conclusion
We have explored some issues surrounding tricks in mathematics. Some questions might be received as tricks and some questions might be solved using tricks.
Questions might be crafted to be received as tricks in various ways, such as wrapping simple content in a new and novel way or making questions using pieces of content which are unfamiliar to the solver. Whether a question is received as a trick often very much depends on the context in which the question is given
A mathematical trick involves a 'light bulb' moment or 'ah' which moves the solver forward. Whether or not a question involves an overt mathematical trick very much depends on the experience of the solver: on first encounter, almost any piece of new mathematical content beyond mere definition might be viewed as a trick. It is only with practice that they are integrated into your repertoire of knowledge and become tools. As you accumulate more content tricks you become a more knowledgable mathematician; as you develop a repertoire of more mathematical process tricks you become a more skilled mathematician. Acquisition of a toolkit of tricks is a valuable and necessary part of the development of mathematical skill.
Footnote
Just as we finished this article we received notification of a new WIKI-style site called 'The Tricki'? (http://www.tricki.org/). This site was recently started by colleagues in the mathematics department here in Cambridge. They say:
'It [The Tricki] can be briefly described as a wiki for mathematical tricks -- hence its name. However, the word "trick" should be interpreted very broadly, and it might be better to use a phrase such as "mathematical technique". It is interesting to reflect how much this description, and the site itself, complements the views expressed in this article.
Appendix: Answers to the questions
1. One. I was going to St. Ives. The others were coming in the opposite direction.
2. 10 (in base 6). The sequence is the same number 6 starting in base 2, then base 3, then base 4 etc.
3. The next letter is J for June. The letters are the first letters of the months of the year
4. Zero. The integrand is an odd function evaluated over the range [-2, 2]. Thus, the positive area will cancel out the negative area.
5. The length of the hypotenuse of the base triangle is 10 (because it is a 6-8-10 triangle. By dropping a perpendicular from the highest point and a line intersecting this at right angles (see diagram below) we see that triangles AXY and ABC are similar. Since the hypotenuse of the larger triangle is double that of the smaller triangle, we see that XY must be half of 8, which is 4. Thus, the total height is 10 .
6. Rearranging we see that $3x = 33$, so $x = 11$.
7. Note that a million equals $(100)^3$, so we are trying to set the sum of two cubes equal to a cube. This is impossible because of Fermat's last theorem.
Stephen Hewson and Jennifer Piggott are both members of the NRICH Project team (nrich.maths.org) , based in Cambridge.