Impuzzable
Solving Impuzzable
Many years ago, when I was still knee high to a grasshopper (er, when I was about 10 probably), I was given a fiendish jigsaw puzzle called Impuzzable. It has only 9 pieces and yet it's the hardest jigsaw puzzle I've ever had. The reason it's so difficult is that there are no edges and no pictures. Here's what it looks like:

Figure 1 - Impuzzable
My family and I tried to solve this puzzle for many months before eventually giving up. Before reading the rest of this article, you might like to have a go at solving it yourself by printing out the jigsaw puzzle and cutting out the shapes. Hopefully this will give you an idea of how fiendish it is!
A few years ago I found the puzzle lying about my house and resolved to defeat it. Rather than spend inordinate amounts of time trying to solve it by hand, I decided to cheat and write a computer program to solve it for me. The rest of this article describes how the program works. It does require some knowledge of programming, but it's written in the easiest programming language of all, BASIC. If you have an oldish PC, it should have come with a copy of QBASIC (at an MSDOS prompt, type "QBASIC" to see if you have this program). If not, you can download it here .
The algorithm
So, how do you you write a computer program to solve a jigsaw puzzle? The most obvious method is to try out every possible way of laying down the 9 pieces in a three by three grid, and checking to see if the edges fit together. Unfortunately, this method could take a very long time, because there are 2,380,855,680 ways of doing this. If you've done any probability or stats at school, you should be able to work out why this is the number of ways of laying the pieces down; if not, don't worry about the next bit. There are 9!=9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 ways of choosing which piece to put in which position. For each piece, there are 4 different ways to rotate it, so for each way of putting the pieces in the available positions, there are 49 different choices of ways to arrange the pieces. So, there are 9! × 49 ways to put down all the pieces.
So that method is too slow, is there a better method? There are probably lots of ways of doing it, but I'll describe the way I chose to do it (a friend of mine has told me that this method is called alpha-beta pruning , which is nice). You lay the first piece down in the first available position. Then you lay the second piece down in the next available position (just underneath it for instance). If it doesn't fit, you rotate it by 90 degrees and try again. If you find a fit, then you pick up the next available piece (the third piece) and place this below the second piece and try different rotations of this piece. If you didn't find a fit for the second piece, you try the third piece underneath the first piece, and so on. Obviously this saves checking millions of ways of laying down all the pieces. In fact, with my program, it only had to check 56,592 arrangements to find every solution to the puzzle! So we've gone from 2 billion arrangements to check all the way down to 60 thousand arrangements to check.
Setting up the data
The first thing we need to do is to turn our puzzle into a form the computer can understand. I've decided the number the pieces as follows:

Figure 2 - Numbered pieces
Now, we need to tell the computer the characteristics of each piece. The important thing about each piece in this puzzle is that it has four sides, and each side can be one of 8 different types; clubs, spades, diamonds and hearts pointing inwards and outwards. I've numbered them in the following way:

Figure 3 - Key
This is a useful way to number pieces, because if we have two edges numbered a and b next to one another, they will fit together if a+b=0 (an edge numbered a only fits with the edge numbered -a ). We'll use this later when writing the actual program.
Now we can label each piece using the key above, here is an example for piece number 1:

Figure 4 - Labelled piece
We'll also give each piece a rotation number, this is a number (0 to 3) which tells us how many times it has been rotated anticlockwise. If the number is 0, it has not been rotated at all, if it's 1 it's rotated 90 degrees anticlockwise, if it's 2 it's been rotated 180 degrees, if it's 3 it's been rotated 90 degrees clockwise, or 270 degrees anticlockwise.
We also number each of the edges of a piece, so that the top edge is edge 1, the right hand edge is edge 2, the bottom edge is edge 3 and the left hand edge is edge 4.
Finally, we number the positions which each piece can be placed in as follows:

Figure 5 - Position numbers
Don't worry about why I've numbered them in that counterintuitive way. I got a bit confused when I originally wrote the program, but it doesn't matter, it's a perfectly good way of numbering the positions.
We've now numbered everything we could possibly want to number. I can specify any way of laying down these pieces purely in terms of numbers. For instance, if I said that piece 1 was in position 5 with rotation number 0, piece 8 in position 4 with rotation number 0 and piece 3 in position 7 with rotation number 1, the board would look like this:

Figure 6 - Example placement
In this example, edge 3 of piece 8 doesn't fit together with edge 1 of piece 1, but edge 4 of piece 8 does fit with edge 2 of the rotated piece 3, which is the same as edge 3 of piece 3 before it's rotated.
Writing the program
The boring bits
Okay, that's the easy bit done. Everything is numbered, now we need to actually write the program that does it. The first thing to do is to set up the pieces, in BASIC, here's how we do it:
DECLARE SUB SetPiece (n!, A!, b!, c!, d!) DIM SHARED P(9, 7) AS INTEGER SUB SetPiece (n, A, b, c, d) P(n, 1) = A P(n, 2) = b P(n, 3) = c P(n, 4) = d 'Keep further copies for rotation! P(n, 5) = A P(n, 6) = b P(n, 7) = c END SUB
Whoa there! What's going on here? Let's go over that and see what we're doing. You can ignore the DECLARE SUB bit, that's just programming details. The DIM SHARED line just sets up an array of integers (whole numbers) in which we're going to store the information about the pieces. So P(4,2) will be the edge type of the 2nd edge of the 4th piece. We want this to be -1 (it's a club pointing inwards). The reason we have 7 edges rather than 4 is for rotations, so that we can work out the edge type of the j-th edge of the i-th piece with rotation number k easily, it's the number P(i,j+k) . Now, the SetPiece subroutine just sets up the piece, the first argument (n) is the number of the piece we're setting up, the next 4 arguments (A,b,c,d) are the edge types of the 4 edges. We can now set up all the pieces like so (you might like to check that you've understood everything so far by working out what the next 9 lines should say yourself):
SetPiece 1, -3, -2, 3, 1 SetPiece 2, 2, 1, -4, -2 SetPiece 3, 4, 2, -3, -2 SetPiece 4, -1, 1, 4, -4 SetPiece 5, -4, 4, 2, -1 SetPiece 6, 1, -1, -2, 2 SetPiece 7, 3, 1, -2, -1 SetPiece 8, -3, -4, 2, 3 SetPiece 9, -4, 3, 3, -2
Next, we set up another array which defines the current positions and rotations of the pieces on the board.
DIM SHARED A(9, 2) AS INTEGER
The number A(n,1) is the number of the piece in position n, the number A(n,2) is the rotation number of this piece. So, for the example board above (included again just below this paragraph), we have A(4,1)=8 A(4,2)=0 A(5,1)=1 A(5,2)=0 A(7,1)=3 A(7,2)=1 .

Figure 6 - Example placement
Next, we define a function to check whether or not two pieces fit together or not.
DECLARE FUNCTION CheckIntersection! (pia!, pa!, pib!, pb!) FUNCTION CheckIntersection (pia, pa, pib, pb) CheckIntersection = ABS(SGN(P(A(pia, 1), pa + A(pia, 2)) + P(A(pib, 1), pb + A(pib, 2)))) END FUNCTION
Ugh! That's a very ugly looking expression, what does it do? First of all, ignore the ABS and SGN bits. ABS just takes the positive value of its input, so ABS(-3)=3 ABS(2)=2. SGN returns the sign of the input, which is -1 if the input is negative, +1 if the input is positive and 0 if the input is 0, SGN(0)=0 SGN(12)=1 SGN(-24)=-1. So, ABS(SGN(x)) is 0 if x is 0 or 1 if x is not 0. Let's just look at this bit of the expression, P(A(pia, 1), pa + A(pia, 2)). This is the edge type of edge pa+A(pia,2) of piece A(pia,1). In other words, this is just the edge type of edge pa of the piece placed in position pia (because A(n,1) is the piece in position n, and A(n,2) is the rotation number of that piece). The next bit, P(A(pib, 1), pb + A(pib, 2)), is just the edge type of edge pb of the piece in position pib. These are added together, so if the two edges fit, the function will return 0, and if they don't fit the function will return 1.
The next bit is a bit tedious, we need another function which will tell us whether or not everything fits after we've put pieces in positions 1 to u. Here goes:
FUNCTION CheckPoss (u)
tot = tot + 1
f = 0
SELECT CASE u
CASE 2
f = f + CheckIntersection(1, 3, 2, 1) 'A
CASE 3
f = f + CheckIntersection(1, 3, 2, 1) 'A
f = f + CheckIntersection(2, 3, 3, 1) 'B
CASE 4
f = f + CheckIntersection(1, 3, 2, 1) 'A
f = f + CheckIntersection(2, 3, 3, 1) 'B
f = f + CheckIntersection(1, 4, 4, 2) 'C
CASE 5
f = f + CheckIntersection(1, 3, 2, 1) 'A
f = f + CheckIntersection(2, 3, 3, 1) 'B
f = f + CheckIntersection(1, 4, 4, 2) 'C
f = f + CheckIntersection(2, 4, 5, 2) 'D
f = f + CheckIntersection(4, 3, 5, 1) 'F
CASE 6
f = f + CheckIntersection(1, 3, 2, 1) 'A
f = f + CheckIntersection(2, 3, 3, 1) 'B
f = f + CheckIntersection(1, 4, 4, 2) 'C
f = f + CheckIntersection(2, 4, 5, 2) 'D
f = f + CheckIntersection(3, 4, 6, 2) 'E
f = f + CheckIntersection(4, 3, 5, 1) 'F
f = f + CheckIntersection(5, 3, 6, 1) 'G
CASE 7
f = f + CheckIntersection(1, 3, 2, 1) 'A
f = f + CheckIntersection(2, 3, 3, 1) 'B
f = f + CheckIntersection(1, 4, 4, 2) 'C
f = f + CheckIntersection(2, 4, 5, 2) 'D
f = f + CheckIntersection(3, 4, 6, 2) 'E
f = f + CheckIntersection(4, 3, 5, 1) 'F
f = f + CheckIntersection(5, 3, 6, 1) 'G
f = f + CheckIntersection(4, 4, 7, 2) 'H
CASE 8
f = f + CheckIntersection(1, 3, 2, 1) 'A
f = f + CheckIntersection(2, 3, 3, 1) 'B
f = f + CheckIntersection(1, 4, 4, 2) 'C
f = f + CheckIntersection(2, 4, 5, 2) 'D
f = f + CheckIntersection(3, 4, 6, 2) 'E
f = f + CheckIntersection(4, 3, 5, 1) 'F
f = f + CheckIntersection(5, 3, 6, 1) 'G
f = f + CheckIntersection(4, 4, 7, 2) 'H
f = f + CheckIntersection(5, 4, 8, 2) 'I
f = f + CheckIntersection(7, 3, 8, 1) 'K
CASE 9
f = f + CheckIntersection(1, 3, 2, 1) 'A
f = f + CheckIntersection(2, 3, 3, 1) 'B
f = f + CheckIntersection(1, 4, 4, 2) 'C
f = f + CheckIntersection(2, 4, 5, 2) 'D
f = f + CheckIntersection(3, 4, 6, 2) 'E
f = f + CheckIntersection(4, 3, 5, 1) 'F
f = f + CheckIntersection(5, 3, 6, 1) 'G
f = f + CheckIntersection(4, 4, 7, 2) 'H
f = f + CheckIntersection(5, 4, 8, 2) 'I
f = f + CheckIntersection(6, 4, 9, 2) 'J
f = f + CheckIntersection(7, 3, 8, 1) 'K
f = f + CheckIntersection(8, 3, 9, 1) 'L
END SELECT
IF f = 0 THEN
CheckPoss = 1
IF u = 9 THEN
PrintSolution
END IF
END IF
END FUNCTION
As I said, this bit is very tedious. If we label the intersection points (i.e. the places where we need to check if two edges fit together) as follows:
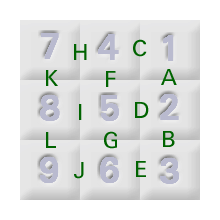
Figure 7 - Intersection points
Now, if we have three pieces on the board in positions 1,2 and 3, then we only need to check intersection points A and B. If we have 4 pieces, we need to check A,B and C. If we have 5 pieces, we need to check A,B,C,D and F. And so on. Where it says tot=tot+1 , this is just keeping count of how many possible solutions we've checked so far. If any intersection points don't match, then f will be bigger than 0, so that's why we have IF f=0 THEN CheckPoss = 1 . If we've put 9 pieces down (u=9) then we've found a solution and we should print it out, here is where the PrintSolution subroutine comes in:
DECLARE SUB PrintSolution ()
SUB PrintSolution
tsol = tsol + 1
c$ = ""
FOR z = 1 TO 9
c$ = c$ + CHR$(A(z, 1) + 64) + CHR$(A(z, 2) + 97)
NEXT
PRINT c$; " ";
PRINT tot
END SUB
You don't really need to worry about this bit, if you're interested you can look up the CHR$ function in your BASIC manual or help file. What it does is it prints out a sequence of two letter strings, the first letter is in capitals and tells you the number of the piece, the second letter is in lower case and tells you the rotation number of the piece. So, if it printed out "AaBbCcDdEaFbGcHdIa", then piece in position 1 is "Aa", which is piece number 1 with rotation number 0, the second piece "Bb" is piece number 2 with rotation number 2. The 9th piece ("Ia") is piece number 9 with rotation number 1.
The interesting bit
Finally, we come to the interesting bit. Here is the function that does the clever stuff:
DECLARE SUB Recurse (n!)
SUB Recurse (n)
m = n + 1
FOR k = 1 TO 9
f = 0
FOR z = 1 TO n
IF A(z, 1) = k THEN f = 1
NEXT
IF f = 0 THEN
FOR r = 0 TO 3
A(m, 1) = k
A(m, 2) = r
i = CheckPoss(m)
IF m < 9 AND i = 1 THEN Recurse m
NEXT
END IF
NEXT
END SUB
Now how does this work? Suppose that we have already laid down n pieces and they all fit together. What this subroutine does is to try all the remaining pieces in the (n+1)th position. The clever bit is that if it can fit a piece into the (n+1)th position, the subroutine runs itself to try and fit a piece in the (n+2)th position, and so on. This is called a recursive function by programmers, which is why the subroutine is called Recurse . The variable k loops through 1 to 9 (FOR k = 1 TO 9), then the program checks if piece k has already been used or not by checking pieces 1 to n (FOR z = 1 TO n, IF A(z,1) = k THEN f = 1, NEXT). If it hasn't been used (IF f=0 THEN) the program checks through all the 4 possible rotation numbers r (FOR r = 0 TO 3). It places the piece in position k with rotation number r (A(m,1) = k, A(m,2) = r) and checks if this fits. If it does fit, it tries to place the next piece by running itself. And that's it! To find the solutions we just need to put the following line in our program:
Recurse 0
Which just means, run the recurse subroutine given that I've placed no pieces so far. Here is the complete listing for this program then, click here to go to the end of the listing:
DECLARE SUB PrintSolution ()
DECLARE FUNCTION CheckIntersection! (pia!, pa!, pib!, pb!)
DECLARE FUNCTION CheckPoss! (u!)
DECLARE SUB Recurse (n!)
DECLARE SUB SetPiece (n!, A!, b!, c!, d!)
'
' Impuzzable Solver
'
COMMON SHARED tot, tsol
tp = 4 ^ 9 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2
DIM SHARED P(9, 7) AS INTEGER
DIM SHARED A(9, 2) AS INTEGER
SetPiece 1, -3, -2, 3, 1
SetPiece 2, 2, 1, -4, -2
SetPiece 3, 4, 2, -3, -2
SetPiece 4, -1, 1, 4, -4
SetPiece 5, -4, 4, 2, -1
SetPiece 6, 1, -1, -2, 2
SetPiece 7, 3, 1, -2, -1
SetPiece 8, -3, -4, 2, 3
SetPiece 9, -4, 3, 3, -2
CLS
PRINT "IMPUZZABLE SOLVER - by Dan Goodman"
PRINT STRING$(80, "-")
Recurse 0
PRINT STRING$(80, " ")
PRINT LTRIM$(RTRIM$(STR$(tot))); " possibilities checked."
PRINT LTRIM$(RTRIM$(STR$((tp - tot) / 1000000))); " million possibilites discarded."
PRINT LTRIM$(RTRIM$(STR$(tsol))); " solutions found."
FUNCTION CheckIntersection (pia, pa, pib, pb)
CheckIntersection = ABS(SGN(P(A(pia, 1), pa + A(pia, 2)) + P(A(pib, 1), pb + A(pib, 2))))
END FUNCTION
FUNCTION CheckPoss (u)
tot = tot + 1
f = 0
SELECT CASE u
CASE 2
f = f + CheckIntersection(1, 3, 2, 1) 'A
CASE 3
f = f + CheckIntersection(1, 3, 2, 1) 'A
f = f + CheckIntersection(2, 3, 3, 1) 'B
CASE 4
f = f + CheckIntersection(1, 3, 2, 1) 'A
f = f + CheckIntersection(2, 3, 3, 1) 'B
f = f + CheckIntersection(1, 4, 4, 2) 'C
CASE 5
f = f + CheckIntersection(1, 3, 2, 1) 'A
f = f + CheckIntersection(2, 3, 3, 1) 'B
f = f + CheckIntersection(1, 4, 4, 2) 'C
f = f + CheckIntersection(2, 4, 5, 2) 'D
f = f + CheckIntersection(4, 3, 5, 1) 'F
CASE 6
f = f + CheckIntersection(1, 3, 2, 1) 'A
f = f + CheckIntersection(2, 3, 3, 1) 'B
f = f + CheckIntersection(1, 4, 4, 2) 'C
f = f + CheckIntersection(2, 4, 5, 2) 'D
f = f + CheckIntersection(3, 4, 6, 2) 'E
f = f + CheckIntersection(4, 3, 5, 1) 'F
f = f + CheckIntersection(5, 3, 6, 1) 'G
CASE 7
f = f + CheckIntersection(1, 3, 2, 1) 'A
f = f + CheckIntersection(2, 3, 3, 1) 'B
f = f + CheckIntersection(1, 4, 4, 2) 'C
f = f + CheckIntersection(2, 4, 5, 2) 'D
f = f + CheckIntersection(3, 4, 6, 2) 'E
f = f + CheckIntersection(4, 3, 5, 1) 'F
f = f + CheckIntersection(5, 3, 6, 1) 'G
f = f + CheckIntersection(4, 4, 7, 2) 'H
CASE 8
f = f + CheckIntersection(1, 3, 2, 1) 'A
f = f + CheckIntersection(2, 3, 3, 1) 'B
f = f + CheckIntersection(1, 4, 4, 2) 'C
f = f + CheckIntersection(2, 4, 5, 2) 'D
f = f + CheckIntersection(3, 4, 6, 2) 'E
f = f + CheckIntersection(4, 3, 5, 1) 'F
f = f + CheckIntersection(5, 3, 6, 1) 'G
f = f + CheckIntersection(4, 4, 7, 2) 'H
f = f + CheckIntersection(5, 4, 8, 2) 'I
f = f + CheckIntersection(7, 3, 8, 1) 'K
CASE 9
f = f + CheckIntersection(1, 3, 2, 1) 'A
f = f + CheckIntersection(2, 3, 3, 1) 'B
f = f + CheckIntersection(1, 4, 4, 2) 'C
f = f + CheckIntersection(2, 4, 5, 2) 'D
f = f + CheckIntersection(3, 4, 6, 2) 'E
f = f + CheckIntersection(4, 3, 5, 1) 'F
f = f + CheckIntersection(5, 3, 6, 1) 'G
f = f + CheckIntersection(4, 4, 7, 2) 'H
f = f + CheckIntersection(5, 4, 8, 2) 'I
f = f + CheckIntersection(6, 4, 9, 2) 'J
f = f + CheckIntersection(7, 3, 8, 1) 'K
f = f + CheckIntersection(8, 3, 9, 1) 'L
END SELECT
IF f = 0 THEN
CheckPoss = 1
IF u = 9 THEN
PrintSolution
END IF
END IF
END FUNCTION
SUB PrintSolution
tsol = tsol + 1
c$ = ""
FOR z = 1 TO 9
c$ = c$ + CHR$(A(z, 1) + 64) + CHR$(A(z, 2) + 97)
NEXT
PRINT c$; " ";
PRINT tot
END SUB
SUB Recurse (n)
m = n + 1
FOR k = 1 TO 9
f = 0
FOR z = 1 TO n
IF A(z, 1) = k THEN f = 1
NEXT
IF f = 0 THEN
FOR r = 0 TO 3
A(m, 1) = k
A(m, 2) = r
i = CheckPoss(m)
IF m < 9 AND i = 1 THEN Recurse m
NEXT
END IF
NEXT
END SUB
SUB SetPiece (n, A, b, c, d)
P(n, 1) = A
P(n, 2) = b
P(n, 3) = c
P(n, 4) = d
'Keep further copies for rotation!
P(n, 5) = A
P(n, 6) = b
P(n, 7) = c
END SUB
The solution
And now we come to the solution, when we run it, the program dutifully chugs and whirs and outputs the following message:
IMPUZZABLE SOLVER - by Dan Goodman
--------------------------------------------------------------------------------
AaHaGcFaCbEcIcDcBb 1103
BdDaIaEaCdFcGaHcAc 12229
GdEdBcHbCcDdAbFbId 44352
IbFdAdDbCaHdBaEbGb 53782
56592 possibilities checked.
95126.758128 million possibilites discarded.
4 solutions found.
But what does this mean? In what sense have I now solved the puzzle? How much more work do we need to do? Well, not much, we just need to decode the somewhat cryptic "AaHaGcFaCbEcIcDcBb" into an actual solution. This string just means (see above for an explanation of why) that in position 1 we have piece 1 with rotation number 0, in position 2 we have piece 8 with rotation number 0, in position 3 we have piece 7 with rotation number 2, and so on. After a bit of work, we get the solution:

Figure 8 - Solution
The other solutions are just what you get when you rotate the whole board around.
Conclusion
I hope you enjoyed that little excursion into the world of programming and jigsaw puzzles. The details can be a bit boring at times (especially checking all the intersection points), but hopefully it's been fun anyway. If you've understood all of the above then you should have got the general idea of how to solve lots of similar puzzles. If you didn't understand some of it, you can post a message on the "Ask NRICH" board.
