Changing Perceptions
Changing students' perceptions of mathematics and of learning mathematics
Changing teachers' perceptions of mathematics and of teaching mathematics
A group of teachers involved in embedding NRICH tasks into their everyday practice were keen to challenge common perceptions of mathematics and of teaching and learning mathematics. In this article, the teachers share what they are doing to change perceptions in their schools.
What were we trying to achieve?
We wanted students to feel positive about learning and doing mathematics through engaging lessons.
Whilst the focus on changing perceptions was initially targeted at learners it became apparent that teachers needed to consider the messages they convey through the way they behave in the classroom, and their expectations of learners. This is dependent on their attitudes towards and beliefs about mathematics and learning mathematics.
NRICH's aim was to offer support that would enable all teachers to provide rich mathematical experiences that highlighted the value of mathematical thinking to all their students. We wanted students and teachers to appreciate that:
- it is not acceptable to say 'I am no good at maths'
- mathematics learning need not depend on teachers demonstrating methods in advance of students practising techniques
- doing mathematics offers an opportunity to be creative, and to share ideas and opinions
- it is acceptable to allow students to flounder a little when solving non-routine problems
- although mathematics can be hard, everyone can experience success
- mathematics is more than a series of isolated and unconnected pieces of knowledge. See, for example, Paul Andrews' article Angle Measurement: an Opportunity for Equity
- mathematics is not just about answers and results, but also about strategies and approaches
- mathematics has cross-curricular connections
- students' perceptions of mathematics can be changed. See, for example, Nardi and Steward's accounts of mathematics being 'TIRED' (Nardi and Steward, 2002a, 2002b, 2003).
- provide time and support to allow teachers and departments to review the messages they give out - what is being promoted and what is being valued in the teaching and learning of mathematics?
- create schemes of work which incorporated NRICH tasks and embedded them in the curriculum
- change the way in which students' mathematical progress was assessed by taking into account their strategies and approaches
- A DVD has been produced with footage of some lessons in which rich tasks have been used. This is being shared at department meetings to focus discussion on what the teacher did and how this might have influenced students' perceptions
- One week every half term is set aside where all lessons for Years 7 and 8 are based around NRICH tasks. The focus is to encourage students to appreciate the value of mathematical thinking and develop more independent ways of working. Issues related to mathematical content are dealt with as they arise.
- Teachers have been working collaboratively, identifying and using NRICH tasks which enhance their well-established scheme of work.
- Lesson plans are used as the starting point for discussions about what is to be taught and how they might be adapted to take into account the different needs of students.
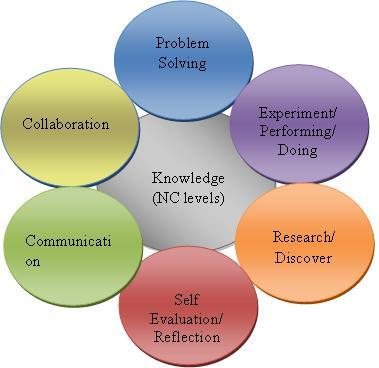
Experience has shown that these assessment criteria allow students to have the full range of their contributions recognised. This is particularly powerful for those students who would have previously considered themselves weak when judged by traditional assessment criteria. This means that a student can achieve credit for several of these skills areas even when a correct solution is not
reached.
Many of the schools encouraged their students to submit solutions to the NRICH problems published each month. NRICH edits and publishes a selection of submitted solutions at the end of each month. It is interesting to note that NRICH only publishes solutions that contain explanations, reasoning and/or justifications. See, for example, the solution to American Billions.
This example solution shows how Zac worked logically to find the number in American Billions.
Let A B C D E F G H I J represent the 10 digits.
The number itself is divisible by 10, so J must be 0.
Since the number formed by the first 5 digits from the left is divisible by 5, E must be 5.
Since AB, ABCD, ABCDEF and ABCDEFGH must be divisible by 2, 4, 6 and 8 respectively, they must all be even. So B, D, F and H are even numbers.
That leaves 1, 3, 7 and 9 for A, C, G and I.
AB could be any of the following: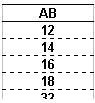
The number formed by the first 3 digits from the left is divisible by 3, so the digits must add up to a number that is divisible by 3.
The possible values of ABC must be: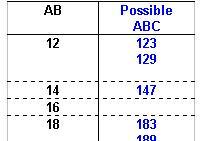
The number formed by the first 4 digits from the left is divisible by 4, so the number formed by the last two digits of the number must also be divisible by 4.
How well are we achieving our aims?
One school has reported a noticeable improvement in behaviour in Years 7 and 8 mathematics lessons since the implementation of these strategies. This has been reflected in a drop in the number of students who have been removed from lessons due to unacceptable behaviour.
Students have indicated in school surveys that they prefer a rich and varied curriculum over a more traditional diet and have shown a greater enthusiasm for mathematics.
Jo Boaler's research evidence shows that a more varied, rich curriculum will not be detrimental to GCSE examination results. See her 2005 and 2006 Journal articles that can be downloaded from http://www.sussex.ac.uk/education/profile205572.html.
Linking to articles:
Nardi E, Steward S (2002) I could be the best mathematician in the world... if I actually enjoyed it. Mathematics Teaching 179: 41-44.
Steward S, Nardi E (2002) I could be the best mathematician in the world... if I actually enjoyed it: part 2. Mathematics Teaching 180: 4-9.
Nardi, E. and Steward, S. (2003) Is Mathematics T.I.R.E.D.? A Profile of Quiet Disaffection in the Secondary Mathematics Classroom, British Educational Research Journal, 29(3), 345-367
This article is the result of the collaborative work of:
Susanne Mallett, Steve Wren, Mark Dawes and colleagues from Comberton Village College
Amy Blinco, Brett Haines and colleagues from Gable Hall School
Jenny Everton, Ellen Morgan and colleagues from Longsands Community College
Craig Barton, Debbie Breen, Geraldine Ellison and colleagues from The Range School
Danny Burgess, Jim Stavrou and colleagues from Sawston Village College
Catherine Carre, Fran Watson and colleagues from Sharnbrook Upper School
David Cherry, Chris Hawkins, Maria Stapenhill-Hunt and colleagues from The Thomas Deacon Academy
Charlie Gilderdale, Alison Kiddle and Jennifer Piggott from the NRICH Project, Cambridge.
For similar articles about teachers using NRICH go here.
