Adding and subtracting positive and negative numbers
This article is an expanded version of one published on NRICH in 2008. The original article is contained within this version.
We are often frustrated when we hear students say "Two minuses make a plus", because it shows a rote-learned phrase that is often misapplied. For example, we have all heard students say things like "minus four minus two equals six, because two minuses make a plus!"
The models for teaching addition and subtraction of positive and negative numbers that we share in this article are designed to lead to understanding. We will make suggestions about how to use language precisely in order to support the understanding of the distinction between operations and directed numbers.
There are four possibilities that we need to be able to understand with our models:
Adding a positive number
Adding a negative number
Subtracting a positive number
Subtracting a negative number
Hot Air Balloon
The first model we offer is the hot air balloon, as seen in the game Up, Down, Flying Around.
In this model, we represent positive numbers as 'puffs' of hot air, and negative numbers as sandbags.
| Model | Calculation | Outcome |
| Adding puffs of hot air | Adding a positive number | Increase (in height) |
| Adding sandbags | Adding a negative number | Decrease (in height) |
| Subtracting puffs of hot air | Subtracting a positive number | Decrease (in height) |
| Subtracting sandbags | Subtracting a negative number | Increase (in height) |
We can now describe a calculation such as 4 + (-2) - (+5) - (-1) + (+7) in the following way:
My balloon starts at height +4. I add two sandbags (down two), subtract five puffs of hot air (down five), subtract one sandbag (up one), then add seven puffs of hot air (up seven). My balloon ends up at height +5.
Eventually, we want students to read the calculation as "Four add negative two, subtract positive five, subtract negative one, add positive seven" (or replacing the operation words add/subtract with plus/minus, but always insisting on positive and negative for the signs accompanying the numbers), and think to themselves "Four, down two, down five, up one, up seven" or equivalent.
Thanks to Alan Mesfin who suggested an alternative of tying on helium balloons (as in the film "Up") instead of adding puffs of hot air to represent adding a positive number.
Happiness Model
Mary Cleare uses a similar approach:
"I believe that adding and subtracting with negative numbers makes sense.
I have a big number line ($^-10$ to $10$, say) above or along the top of my whiteboard. With the students, we brainstorm on things that are POSITIVE and things that are NEGATIVE. We talk about how you feel if someone gives you a positive thing, or if someone takes one away. We talk about how you feel if someone gives you a negative thing, or if someone takes one away.
I feel OK today, maybe I score $2$ (pointing to number line) on this happiness scale.
How would I feel if someone gave me $4$ chocolates (a generic positive!)? Yes, I move up $4$ to $6$.
Now how would it be if someone gave me a detention (negative)? Yes, down $1$, to $5$.
What if you took away $7$ of my chocolates? How would I feel? Sadder? Yes, I need to go down $7$, to $^-2$.
What if you gave me $3$ detentions? Etc.
At some point, I usually get all the students pointing the direction I should be moving along the scale, so it's easy to see who hasn't got the idea yet. Once the class are getting confident, I usually start recording some of the calculations on the board, or getting a student to do it for me! I usually let them suggest moves that will take my happiness off the scale that I happen to have on my number line.
As a finale before I ask them to do lots of standard + and - questions, we make up a problem like:
$6 - (^+7 )+ (^-2) -(^+1) - (^-4) + (^+9) + (-3) -(^+1) - (^-7) - (^+4) - (^-8) =$ ?
to do together.
Football Model
In this model, we represent positive numbers as good footballers who score lots of goals, and negative numbers as bad footballers who score own goals. When it's time for transfers, we can add new players to our team, or take players off the team.
| Model | Calculation | Outcome |
| Buy good players | Adding a positive number | Increase (in league position) |
| Buy bad players | Adding a negative number | Decrease (in league position) |
| Sell good players | Subtracting a positive number | Decrease (in league position) |
| Sell bad players | Subtracting a negative number | Increase (in league position) |
So imagine we bought 5 good players, sold 2 good players, bought 3 bad players and sold 7 bad players. We can write the following calculation to find out the overall effect:
$+(^+5) - (^+2) + (^-3) - (^-7)$
So overall, we improve our position by 7.
In all of these models, we use an analogy where adding something positive or subtracting something negative improves the situation (happier, higher league position, balloon rising up).
In some ways, it doesn't matter which model you use, as long as you are pedantic about using the correct language to separate operations from directed numbers, and relate the model to the calculations. We would advise choosing one (or at most two) models at first, to avoid confusing students with lots of conflicting images.
The problem Strange Bank Account uses the context of depositing and withdrawing money, but does not have such a strong analogy to explain all four possibilities captured in the tables above. However, it can be used to introduce the concept of directed number, and then used in conjunction with another model.
Finally, we offer a more abstract way of looking at the addition and subtraction of positive and negative numbers, without relying on an analogy:
Counters Model
This model was introduced to us by Don Steward.
Let this be $4$

and this

and this
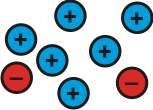
and this
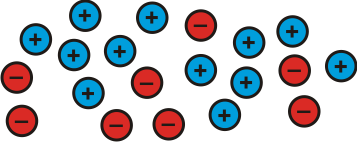
Students could be asked to suggest some other possibilities.
Can they explain why they all represent $4$?
Let this be $^-2$
and this

and this

and this

Students could be asked to suggest some other possibilities.
Can they explain why they all represent $^-2$?
This is $3$
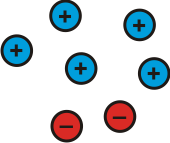
When we partition it we can make different sums:
Image
| $2 + 1 = 3$
$3 - 2 = 1$
$3 - 1 = 2$ | Top + Bottom = Whole
Whole - Top = Bottom
Whole - Bottom = Top |
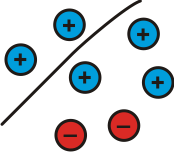
If we partition it differently we can make different sums:
Image
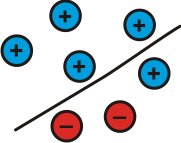
| $4 + (^-1) = 3$
$3 - 4 =$ $^-1$
$3 - (^-1) = 4$ | Top + Bottom = Whole
Whole - Top = Bottom
Whole - Bottom = Top |
Image
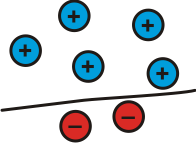
| $5 + (^-2) = 3$
$3 - 5 =$ $^-2$
$3 - (^-2) = 5$ | Top + Bottom = Whole
Whole - Top = Bottom
Whole - Bottom = Top |
This is $^-4$
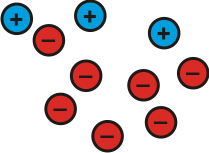
Image
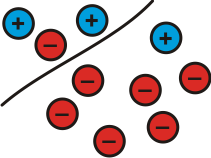
| $1 + (-5) =$ $^-4$
$^-4 - 1 =$ $^-5$
$^-4 - (^-5) = 1$ | Top + Bottom = Whole
Whole - Top = Bottom
Whole - Bottom = Top |
If we partition it differently we can make different sums:
Image
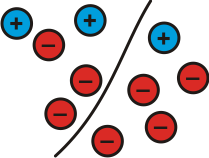
| $^-1 + (^-3) =$ $^-4$
$^-4 - (^-1) =$ $^-3$
$^-4 - (^-3) =$ $^-1$ | Top + Bottom = Whole
Whole - Top = Bottom
Whole - Bottom = Top |
Students could be asked to create three different sums based on their partitions of other sets of pluses and minuses.
How can this model help us make sense of adding negative numbers?
We can add a negative number to a positive number and end up with a positive solution:
| $6 + (^-2)$ | = | ? |
Image

| = | Image

|
| $6 + (^-2)$ | = | 4 |
We can add a negative number to a positive number and end up with a negative solution:
| $4 + (^-6)$ | = | ? |
Image

| = | Image

|
| $4 + (^-6)$ | = | $^-2$ |
We can also add a negative number to a negative number:
| $^-2 + (^-3)$ | = | ? |
Image

| = | Image

|
| $^-2 + (^-3)$ | = | $^-5$ |
Students could be asked to create a few more additions like the ones above.
Gathering various results may then offer an opportunity to ask students what they notice.
Can they suggest how to add negative numbers without going to all the trouble of drawing pluses and minuses
How can this model help us make sense of subtracting negative numbers?
We can subtract a negative number from a negative number and end up with a negative solution:
Consider $^-8 - (^-3)$:
| This represents $^-8$ | Image

|
And this represents $^-8$ subtract $^-3$ | Image
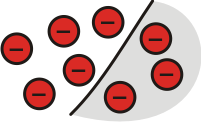
|
| Leaving us with $^-5$ | Image

|
So $^-8 - (^-3) =$ $^-5$
Can we subtract a negative number from a positive number?
Let's consider $5 - (^-2)$ = ?
How can we take $^-2$ from $5$?
Image

| represents $5$ |
| but so does this | Image

|
Now we can take $^-2$ from $5$ and we will be left with:

So $5 - (^-2) = 7$
We can subtract a negative number from a negative number and end up with a positive solution!
Let's consider $^-4 - (^-7)$ = ?
Image

| represents $^-4$ |
| but so does this | Image

|
Now we can take $^-7$ from $^-4$ and we will be left with:
So $^-4 - (^-7) = 3$
Students could be asked to create a few more subtractions like the ones above.
Gathering various results may then offer an opportunity to ask students what they notice.
Can they suggest how to subtract negative numbers without going to all the trouble of drawing pluses and minuses?
If you have a SMART Board, you may wish to download this notebook file which was shared with us by Jon Turpin.
