Same Shapes
Problem
Look at this shape. The dotted line shows how it can be cut in half to make two shapes that are the same shape and size.
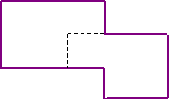
How can these shapes be cut in half to make two shapes the same shape and size?
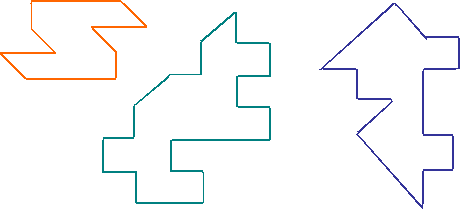
Can you find more than one way to do it?
You may find it helpful to print off this sheet which has three copies of each shape on it.
Getting Started
You could cut the shape to check whether the two parts are identical.
Student Solutions

A correct set of solutions was sent in by Christina (Malborough Primary School, UK), Ceren, Idi, Ece, Eda and Ece O (Private IRMAK Primary & Secondary School, Istanbul, Turkey).
Some managed to find two different ways to halve the orange S shape, and Jason (Priory School) found all four ways.
Evren and Christian (Private IRMAK Primary & Secondary School, Istanbul, Turkey) sent in one that no-one else found:

Thomas (Tattingstone School UK) says there are an infinite number of lines that can be drawn like the ones below.

What do think? Are there more solutions for this shape?
Why are there so many for this one and not the other shapes?
Teachers' Resources
Why do this problem?
This activity will be very useful when wishing to challenge and extend pupils' spatial awareness with 2D shapes. It can also be an exercise in perseverence.
Possible approach
The problem Happy Halving might be suitable to start with, before tackling the shapes in this problem. There are detailed suggestions of an approach in the teachers' notes of Happy Halving.
Key questions
Are you able to show me that your two halves are the same shape and size?
Are there other ways of halving this shape?
Possible extension
Some learners will enjoy inventing some shapes of a similar nature. Make sure they test their own shapes to check they work!
Possible support
Ideally, pupils could work in pairs so they can share ideas with each other.
