The dice train
This dice train has been made using specific rules. How many different trains can you make?
Age
7 to 11
Challenge level
Problem
Image
This dice model represents an old blue steam train with a white funnel on the engine at the front. The dice that make up the train are joined using three rules.
RULE 1: Faces that touch each other have the same number.
So, underneath the white dice is a $3$ touching a $3$ on the blue dice.
The blue dice has a $6$ on the face that touches the $6$ on the middle blue dice.
The middle blue dice has a $1$ that touches the $1$ on the last dice.
RULE 2: The number on the top of the funnel must equal the total of the numbers showing on top of the remaining dice (carriages) that can be seen.
So, the $4$ on top of the funnel equals the two $2$'s on top of the blue carriages.
RULE 3: Always use four or more dice - so you have at least two 'carriage numbers' to add up.
YOUR CHALLENGE
Obeying all the rules, how many solutions are possible?
You can make models like this one or you could make it longer.
Each one you make is to have the funnel on top of the front dice.
This problem featured in a preliminary round of the Young Mathematicians' Award.
Student Solutions
Students from the Mathematics Extension Program (MEP) at Lumen Christi School in Australia sent in the following:-
Having previously attempted the Add Three Dice Challenge we were confident of finding multiple solutions to this problem.
To begin we used different sized six-sided dice from around the Mathematics resource room and began trying various combination. After checking to see if each train met the two criteria we took a photo of the finished product.
After a while we decided to develop a recording system to ensure we were not repeating any combinations.
Image
Image
Hayden began investigating finding solutions that involved using more carriages. Soon other students took up this challenge.
Image
Image
Image
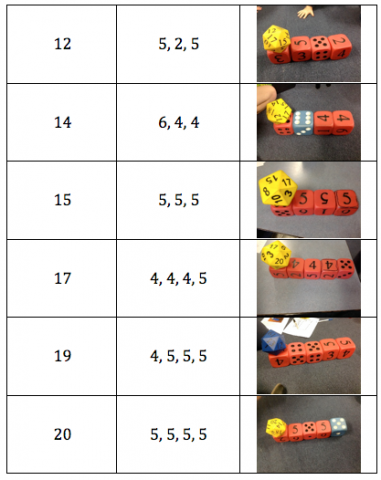
Hayden explained to the group that the final combination above: 6 - 1, 1, 1, 1, 1, 1 is the longest train that can be created using the initial criteria of having 6-sided dice.
From here, students began to extend the problem by investigating whether or not they could find any solutions that still fulfilled the criteria, but used more dice or at least one dice that had more than 6 sides. Flynn was able to find and justify the first solution and soon other students followed. Flynn explained that under the black 8 is a 1, which matches with the 1 on the orange dice.
Image
Image
Image
Julian suggested we could make a train that met the criteria, but had a taller funnel.
Image
This suggestion prompted Jerusha to create a train that fulfilled the criteria, but had a wider funnel:
Image
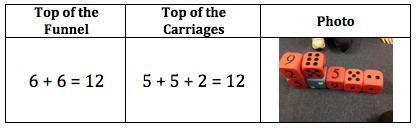
All up we found 18 solutions to the original problem and 14 solutions to different variations of the problem.
Thank you very much, an excellent thinking and well illustrated.
Haaziq Sheikh, Ethan Yu, Nanayaw Nyarko-Bonsu from Priorslee Primary Academy wrote:-
What we did.
We got four dice and we focused on the last two carriages. So we had 3 and 2 connected with 1. We knew that the opposite numbers on all even dice add up to 7. As 7 minus 5 equals 2, we knew that the third dice had to have 2 on top and had to be connected by 6 because, as the other connection was 1, 7 minus 1 equals 6. Then we got 2 to connect with two of the odd
coloured dice and got 5 on top which is correct as 3 plus 2 equals 5.
We Learnt That:
opposite sides of a dice add up to 7
Thank you all of you for your submissions. If you've not tried this yourself have a go. You could follow the first solutions and start altering a rule to explore further.
Teachers' Resources
THE DICE TRAIN
Image
This dice model represents an old blue steam train with a white funnel on the engine at the front. The dice that make up the train are joined using two rules.
RULE 1: Faces that touch each other have the same number.
So, underneath the white dice is a $3$ touching a $3$ on the blue dice.
The blue dice has a $6$ on the face that touches the $6$ on the middle blue dice.
The middle blue dice has a $1$ that touches the $1$ on the last dice.
RULE 2: The number on the top of the funnel must equal the total of the numbers showing on top of the remaining dice (carriages) that can be seen.
So, the $4$ on top of the funnel equals the two $2$'s on top of the blue carriages.
RULE 3: Always use four or more dice - so you have at least two 'carriage numbers' to add up.
RULE 1: Faces that touch each other have the same number.
So, underneath the white dice is a $3$ touching a $3$ on the blue dice.
The blue dice has a $6$ on the face that touches the $6$ on the middle blue dice.
The middle blue dice has a $1$ that touches the $1$ on the last dice.
RULE 2: The number on the top of the funnel must equal the total of the numbers showing on top of the remaining dice (carriages) that can be seen.
So, the $4$ on top of the funnel equals the two $2$'s on top of the blue carriages.
RULE 3: Always use four or more dice - so you have at least two 'carriage numbers' to add up.
YOUR CHALLENGE
Obeying all the rules, how many solutions are possible?
You can make models like this one or you could make it longer.
Each one you make is to have the funnel on top of the front dice.
Why do this problem?
This problem challenges pupils in a novel situation, which may seem simple at first. It combines spatial awareness and number awareness.Possible approach
Introduce dice to the children by asking what they already know about them. You could then talk about what numbers are visible when they are on a table. Next, make the train shape using differently coloured dice and talk about what numbers are on top.
When they are happy with that, introduce the rule about the 'funnel number' and the 'carriages numbers'. They can then talk about the numbers that face each other. When they are comfortable with the rules they can start setting about finding examples that work.
You may wish to stop at a suitable moment to bring the children back together for a short time (a mini plenary). You could ask children to share ways of working which may help all learners in the group progress.
Tell me how you are finding more solutions.
When they are happy with that, introduce the rule about the 'funnel number' and the 'carriages numbers'. They can then talk about the numbers that face each other. When they are comfortable with the rules they can start setting about finding examples that work.
You may wish to stop at a suitable moment to bring the children back together for a short time (a mini plenary). You could ask children to share ways of working which may help all learners in the group progress.
Key questions
What numbers have you got that equal each other?Tell me how you are finding more solutions.