Penta Place
Problem
Penta people, the Pentigles, always build their houses from five square rooms on one level - ground level.
The houses can be designed in a variety of shapes, but a room must be joined to at least one other room by one wall.
Here is a design drawing for a Penta house, a view from above.
![]()
Here is another one:

There are many different ways that you can arrange the five rooms.
I wonder how many different Penta homes you can create.
Try to find all possible shapes the Pentigles can build their homes.
New homes are being built in Penta Place.
The homes are built right next to each other and are arranged and fitted together to create other shapes. Experiment and see what shapes you are able to make.
Penta Place will use just one shape that can be made, the rectangle.
See if you can solve some of the Penta's challenges below.
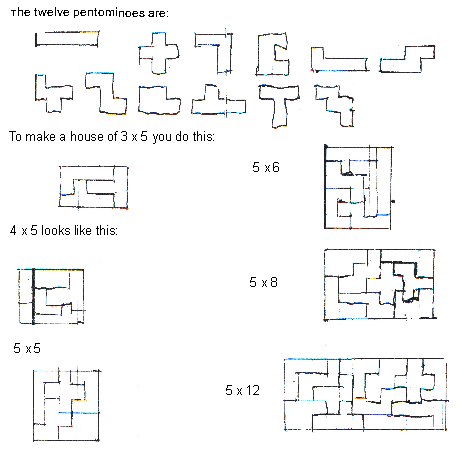
Find three of the Penta house shapes that you created and fit them together to form a 3X5 rectangle like this one.
I wonder if you could make other sized rectangles using three of the Penta shapes.

Are you able to find four of the Pentigles' house shapes to make a larger rectangle like this?

Here we have a 5 by 5 square. Construct a similar square with five of the Penta houses.

If you are unable to do these activities, check that you have made all of the Pentigles' house shapes that you possibly can.
There are in fact 12 different shapes. Have you found all of them?
Now, try to find six of the Penta houses and arrange them to fit into a 5X6 rectangle like this one.

This arrangement might require a more work, but can you find eight of your Penta designs to recreate a 40 room unit arranged in an 5X8 rectangle?

I wonder whether a rectangle can be constructed using 9, 10 or 11 of the Penta shapes....
By now you should have managed to find all of the Penta shapes.
This large rectangle is made from 60 rooms. Here is a very difficult challenge! Can you use all 12 Pentomino shapes to make a similar rectangular arrangement.

I wonder what results you would get if you arranged the houses into shapes other than rectangles .....
Printable NRICH Roadshow resource.
Student Solutions
Madras College have done a lot of work on this problem and Malcolm sent us some nice solutions: