Maze 100
Can you go through this maze so that the numbers you pass add to exactly 100?
Problem
In this maze there are numbers in each of the cells. You go through adding all the numbers that you pass. You may not go through any cell more than once.
Can you find a way through in which the numbers add to exactly 100?
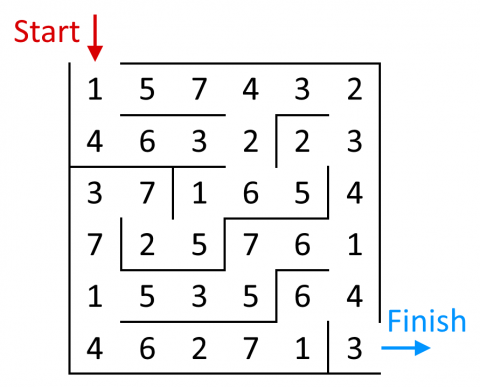
What is the lowest number you can make going through the maze?
What is the highest number you can make going through the maze? (Remember you may not go through any cell more than once.)
Getting Started
Try making a list of the numbers as you pass them.
You could do each route in a different colour.
You can print out two copies of the maze from this sheet.
Student Solutions
Hollie from Gresham Primary School offered the following general advice when tackling this task:
I have three strategies I used.
1) You can start by drawing a random line then add up mentally or write it down. However, if you're trying to get 100 don't go straight round the outline because it will be too small.
2) Add the numbers up as you go and make a note of totals when you get to corners. Then if you need to make the final answer bigger or smaller you can just go back to the last corner to change the route.
3) The main thing is even if you don't get it straight away is be creative, resilient and persevere. Don't forget to check your adding!!
What fantastic tips, Hollie, thank you.
Bonner Primary School sent in this commentary:
Thoughts before we started:
Aarfin: I think you have to use a lot of numbers to make 100.
Aadil: I am going to add all the numbers to check it comes to more than 100.
Thoughts as we began:
Tahir: I think this will be easy, I made 98 I just need 2 more.
Sakinah: I will do my best and never give up. I say this to myself so I don't feel discouraged.
Thoughts after 20 minutes
Tahir: I thought it was easy but it's hard. I think I need to find the bigger numbers.
Sakinah: I went the long way round to find the answer.
Sophia and Abu: We decided to add up all the numbers then see which ones we needed to take away to make 100. This was hard!
Aadil and Azreen solved the maze first.
Jess and Suja from Harrisons School explained the way they approached the task:
To solve the Maze 100 problem we used a systematic approach. We started off by drawing all of the possible routes from the start to the end of the maze and colour coded them to make them clear. Then we added up the numbers along those route separately so we could find which one added up to 100. From finding all of the routes and adding them up it was easy to find out the highest and lowest as we had all of the information ready.
Hugo and Josh, and Finn and Ben, also from Harrisons School, sent in very clear solutions. Here is Catrin and Abi's. It is not totally correct, but we thought it worth including as they worked hard to try to find all the possible routes through the maze (there are some comments underneath which will help you spot the errors):

Well done, Catrin and Abi. I think there are a few slip-ups in their solution:
- I wonder whether they have missed out one possible route;
- The totals of numbers 1, 2, 3, 4, 5 and 8 are not quite right, which affects the lowest possible total and means there may be another solution to the challenge of making 100 (!);
- I think in solution number 6, there is a 6 missing near the end (but the total is correct).
Sonja sent in a link to a video in which she talks through her findings.
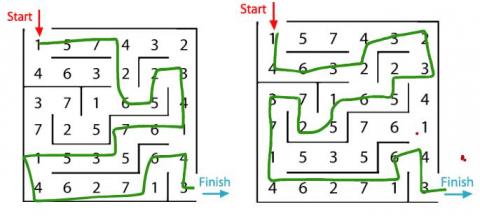
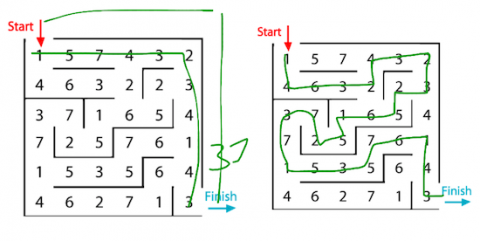
She found two ways to make 100. She also found the lowest route of 37 and the highest route of 101. The video can be viewed at www.educreations.com/lesson/view/maze-100/23257143/?s=NXNLIp&ref=link
Here is an image of the two ways Sonja found of making a total of 100:
Here is an image of the routes Sonja found with the smallest and largest totals:
Well done, Sonja!
Isabelle and Takumi from Monarch Global Academy, USA; children at Cefnllys-Llandrindod County Primary School in Wales; Lea and Ayla from Torriano Primary School; Mariah from Stimpson Avenue Academy; Frida, Steven, Harsh, Yuha, Matthew and Zoe from Nord Anglia International School Hong Kong; Kaitlyn from St.Helen's Primary School; Liam and Olivia from Millfields Primary School; Year 4 from Britannia Primary School; Bryon and Grace Kaiapoi North School in New Zealand; Jamie and James from Sheuchan Primary School in Scotland; Max from Dussindale Primary School; Leila, Amaya, Aoife, Saachi from North London Collegiate School; Advika from Wimbledon Chase Primary School, Thomas, Cayden, Rudi, Emilia, Matthew and others from Hempland Primary and James from St Williams Primary School all sent in good solutions too.
Teachers' Resources
Why do this problem?
This problem uses a maze as a context in which to practise addition and to work in a systematic way. In the past many comics, annuals and 'children's corners' in newspapers had a maze of some sort but they are less common now. As a result, some children may not have come across mazes like this so they may need some explanation of what to do. You might like to print off a sheet containing two copies of the maze.
Possible approach
Show the maze on screen and then ask the class to watch you carefully. Don't say anymore, but draw out a route through the maze, one number at a time, and each time you go through a new number, write up the running total on the board. Do all this in silence until you reach the exit of the maze and have your final total. Then give learners chance to talk in pairs about what they think you were doing.
Use a whole class discussion to clarify the 'rules' of the task and then challenge them to find a total of 100, working in pairs. Give some time for learners to work on the problem, then draw everyone together for a mini plenary. Ask pupils to describe how they are tackling the task. This will allow some children to articulate their thinking so far, and therefore help to clarify their thoughts, whereas for others it will be a chance to hear what other pairs have done so helping them 'get off the ground'.
Having shared some strategies, walk around the room as children work, listening out for those who are forming reasoned arguments for their route, as opposed to those who are working more haphazardly. In addition, look out for pairs who begin to 'tweak' solutions to get nearer to 100, rather than beginning again from scratch.
Key questions
Tell me about your journey through the maze.
How are you choosing where to go next?
What do you notice about the structure of the maze?
How could you adjust your journey to get closer to 100 rather than starting again at the beginning?
How will you record what you have tried?
How is your recording supporting you to solve this challenge?
Possible extension
You could ask questions such as:
- Is there more than one way through the maze that totals 100?
- What is the highest total? Lowest total?
- Can you go through the maze and make a total that is a multiple of 10? A prime number?
Pairs of children might like to set their own end totals as a challenge for each other.
Learners could make up an even harder maze than this with these numbers in it.
Mazes can be made any shape and can be based on squares, circles, triangles and hexagons.
Or learners could design a different maze where the numbers were decimals and the challenge was to travel through the maze and emerge with a total of 10.
Possible support
Challenge learners to find an accurate total for their journey through the maze. Children may like to use a beadstring to help with the addition and help keep a running total.
